Kovarianz verstehen und berechnen - mit Formel und Beispiel
Die Kovarianz gibt dir Auskunft über den Zusammenhang von zwei metrischen Variablen.
Dabei ist es wichtig, zu beachten, dass die Kovarianz ein nichtstandardisiertes Zusammenhangsmaß ist und damit nur begrenzt vergleichbar.
Andere Bezeichnungen für die Kovarianz sind Stichprobenkovarianz oder empirische Kovarianz.
Die Berechnung der Kovarianz am Beispiel erklärt
Nehmen wir an, wir haben acht Personen nach der Entfernung zwischen ihrem Wohn- und Arbeitsort und der Dauer ihres Arbeitsweges gefragt und folgende Daten erhalten:
| Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Entfernung Wohnort und Arbeitsplatz in km | 18 | 2 | 42 | 14 | 22 | 35 | 45 | 8 |
| Dauer des Arbeitsweges in min | 22 | 10 | 53 | 30 | 25 | 36 | 45 | 13 |
Nun möchten wir den Zusammenhang zwischen den beiden Variablen bestimmen und berechnen dazu die Kovarianz.
Als Ergebnis erhalten wir eine Kovarianz von 222.93, was bedeutet, dass ein positiver Zusammenhang zwischen den beiden Variablen ‚Entfernung‘ und ‚Dauer‘ besteht.
Die Tabelle gibt dir einen Überblick über die einzelnen Schritte zur Berechnung der Kovarianz.
Schritt-für-Schritt-Erklärung zur Berechnung der Kovarianz
| Allgemein | Beispiel | ||||||||||||||||||||||||||||
| 1 | Bestimme das arithmetische Mittel für jede der Variablen. | 1. Entfernung Wohnort zum Arbeitsplatz (x)
2. Dauer des Arbeitswegs (y) |
|||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | Berechne die Abweichungen der einzelnen Beobachtungsdaten vom arithmetischen Mittel, z. B. |
|
|||||||||||||||||||||||||||
| 3 | Bilde das Produkt der Abweichungen.
Rechne also: |
Wir multiplizieren das Ergebnis aus der mittleren Spalte aus Schritt 2 mit dem Ergebnis aus der rechten Spalte.
|
|||||||||||||||||||||||||||
| 4 | Bilde die Summe aller Produkte aus Schritt 3. | Wir addieren alle Ergebnisse aus Schritt 3:
38.06 + 409.06 + 445.31 + (-6.94) + 5.31 + 79.31 + 342.56 + 247.81 = 1560.48 |
|||||||||||||||||||||||||||
| 5 | Multipliziere das Ergebnis aus Schritt 4 mit |
Die Kovarianz beträgt 222.93. |
Formel zur Kovarianz
Die Formel stellt die oben erläuterten Schritte zur Berechnung der Kovarianz zusammengefasst dar.
| sxy | Kovarianz der Variablen x und y |
| n | Gesamtanzahl der Beobachtungen |
| xi | Beobachtungswert der Variable x |
| x̄ | arithmetisches Mittel der Variable x |
| yi | Beobachtungswert der Variable y |
| arithmetisches Mittel der Variable y | |
Interpretation der Kovarianz
Ein positiver Wert der Kovarianz sagt dir, dass wenn die eine Variable steigt, dies auch für die andere der Fall ist. Gleichermaßen zeigt ein negatives Vorzeichen, dass wenn die eine Variable steigt, die andere sinkt.
In dem Beispiel zur Entfernung zwischen Wohn- und Arbeitsort und zur Dauer des Arbeitsweges beträgt die Kovarianz 222.93.
Dieses Ergebnis zeigt uns, dass ein positiver Zusammenhang besteht. Wenn also die Variable ‚Entfernung‘ steigt, ist dies auch für die Variable ‚Dauer‘ der Fall.
Genauso bedeutet ein Anstieg der Variable ‚Dauer‘ ebenfalls einen Anstieg der Variable ‚Entfernung‘.
Von der Kovarianz zur Korrelation
Da die Kovarianz eine nichtstandardisierte Kennzahl ist, ist die Vergleichbarkeit gering. Um konkrete Schlüsse und Vergleiche zu ziehen, können wir die Kovarianz in einen Korrelationskoeffizienten umwandeln.
Dazu verwenden wir die folgende Formel:
| sxy | Kovarianz der Variablen x und y |
| sx | Standardabweichung der Variable x |
| sy | Standardabweichung der Variable y |
| r | Korrelationskoeffizient (nach Bravais) |
Beispielrechnung von der Kovarianz zur Korrelation
In unserem Beispiel haben wir eine Kovarianz von 222.93 berechnet und können außerdem über die Formel der Standardabweichung folgende Werte bestimmen:
sx = 15.86
sy = 14.95
Diese setzen wir in die Formel ein, um aus der Kovarianz den Korrelationskoeffizienten zu erhalten:
Die Korrelation zwischen den beiden Variablen ‚Entfernung‘ und ‚Dauer‘ beträgt 0.94. Da es sich bei der Korrelation um einen standardisierten Wert handelt, können wir nun unser Ergebnis mit anderen Korrelationen vergleichen.
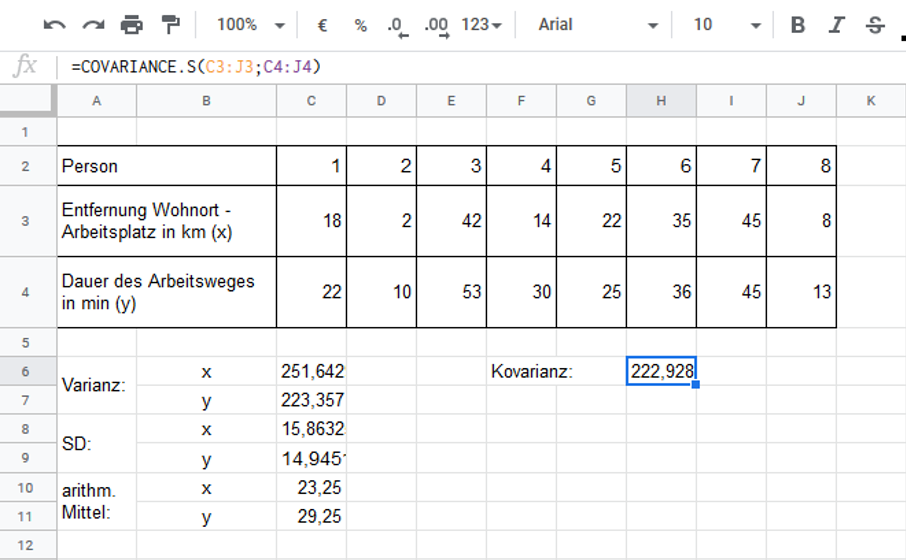
Kovarianz in Excel bestimmen
In Excel können wir die Kovarianz zweier Variablen mithilfe der Funktion KOVARIANZ bestimmen.
Schreibe dazu =KOVARIANZ oder =COVARIANCE und gib in den Klammern die Zellen mit den Werten an, für die du die Varianz bestimmen willst.
Da wir in unserem Beispiel die Kovarianz für die Variablen ‚Dauer‘ und ‚Entfernung‘ bestimmen wollen, fügen wir C3:J3;C4:J4 in den Klammern ein. Als Ergebnis wird uns die Kovarianz von 222.93 angezeigt.
Häufig gestellte Fragen
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2022, 12. September). Kovarianz verstehen und berechnen - mit Formel und Beispiel. Scribbr. Abgerufen am 2. Juli 2025, von https://www.scribbr.de/statistik/kovarianz/

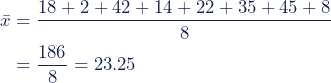
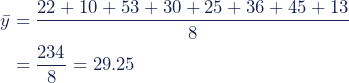
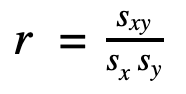 .
.