Annahmen für statistische Tests erklärt mit Beispielen
Für statistische Tests wie die Regressionsanalyse, den t-Test oder die ANOVA werden bestimmte Annahmen vorausgesetzt.
Es ist wichtig, diese Annahmen zu überprüfen. Du kannst nur richtige Schlüsse aus den Ergebnissen deiner statistischen Analysen ziehen, wenn diese Annahmen eingehalten werden.
Annahme 1: Lineare Beziehung zwischen Variablen
Wenn du eine lineare Regression durchführst, ist es wichtig, dass die Beziehung zwischen der erklärenden und der abhängigen Variable linear ist. Das bedeutet, dass der Einfluss der erklärenden Variable sowohl für niedrige als auch für hohe Werte derselbe sein muss.
Lineare Beziehung überprüfen
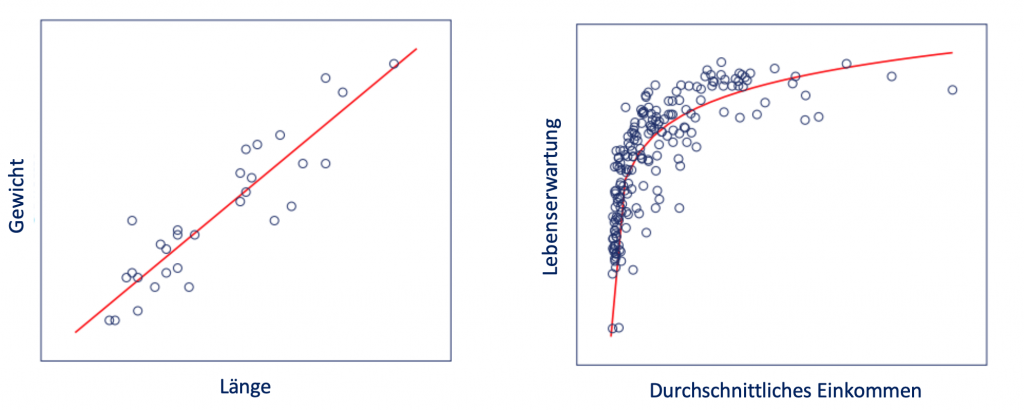
Um zu testen, ob sich 2 Variablen linear aufeinander beziehen, erstellst du ein Streudiagramm. Wenn du zwischen den Datenpunkten eine beinahe gerade Linie ziehen kannst, besteht ein linearer Zusammenhang.
Um in SPSS ein Streudiagramm zu erstellen, klicke auf:
- Grafik
- Diagrammerstellung
- Streu-/Punktdiagramm
Im linken Streudiagramm liegen die Datenpunkte annähernd auf einer geraden Linie. Der Einfluss der Größe auf das Gewicht ist für alle Datenpunkte konstant. Es besteht eine lineare Beziehung.
Im rechten Streudiagramm kann keine gerade Linie die Punktewolke miteinander verbinden. Es besteht kein linearer Zusammenhang.
Vorgehensweise bei nicht bestätigter linearer Beziehung
Wenn keine lineare Beziehung zwischen den Variablen existiert, kannst du das Quadrat oder den Logarithmus einer Variable in die Regression einbeziehen, indem du die Variable transformierst.
Der Vorteil davon ist, dass der Effekt der erklärenden Variable auf die abhängige Variable besser geschätzt werden kann. Die Interpretation der Regressionskoeffizienten wird dadurch aber etwas schwieriger.
Annahme 2: Zufallsstichprobe
Wenn du empirische Forschung durchführst, sammelst du häufig Daten über deine Stichprobe. Du möchtest dann die Resultate der Stichprobe für die Grundgesamtheit generalisieren. Damit das möglich wird, ist es wichtig, dass deine Stichprobe zufällig ausgewählt wurde und dieselben Eigenschaften wie die Grundgesamtheit aufweist.
Unabhängige Beobachtungen
Die Personen müssen zufällig gewählt werden, aber auch unabhängig voneinander sein. Das bedeutet, dass eine Beobachtung nicht eine weitere beeinflussen darf.
Anders als die anderen Annahmen in diesem Artikel kann die Voraussetzung der Zufallsstichprobe nicht getestet werden. Stattdessen musst du kritisch hinterfragen, wie du deine Stichprobe ausgewählt hast.
Annahme 3: Keine Multikollinearität
Eine starke lineare Beziehung zwischen den erklärenden Variablen wird als Multikollinearität bezeichnet.
Multikollinearität kann dazu führen, dass deine Regressionskoeffizienten in deinem Regressionsmodell unzureichend geschätzt werden.
Denn die erklärenden Variablen sagen einander voraus, und dadurch kann keine zusätzliche Varianz in deinem Regressionsmodell erklärt werden.
Ebenso wenig kannst du eine Kombination aus verschiedenen Variablen verwenden, die sich aufeinander beziehen.
Auf Multikollinearität in SPSS testen
Wenn du eine Regressionsanalyse in SPSS durchführst, kannst du unter Statistiken – Kollinearitätsdiagnose auswählen. Der VIF (engl. Variance Inflation Factor) wird in der SPSS-Ausgabe unter Koeffizienten – Kollinearitätsstatistik angezeigt.
Als Faustregel gilt, dass ab einem VIF-Wert von 5 ein Problem im Zusammenhang mit dem Abschätzen des Regressionskoeffizienten der relevanten Variable besteht.
Der VIF-Wert ist nur für die erklärenden Variablen in deinem Modell wichtig. Ein hoher VIF-Wert für die Kontrollvariablen ist kein Problem.
Vorgehensweise bei Multikollinearität
Wenn Multikollinearität besteht, ist es sinnvoll, die korrelierenden Variablen in einem übergeordneten Konzept zu kombinieren. Du kannst dafür Cronbach’s Alpha verwenden oder eine Faktorenanalyse durchführen.
Annahme 4: Exogenität
Exogenität bedeutet, dass die abhängige Variable von der erklärenden Variable und der Störgröße abhängt.
Das Gegenteil zu Exogenität ist Endogenität, die vermieden werden muss, wenn du Aussagen über den Effekt der Variable A auf die Variable B (Kausalität) machen möchtest.
Der Effekt der erklärenden Variable auf deine abhängige Variable wird mit dem Regressionskoeffizienten geschätzt. Im Fall von Endogenität lässt sich der Regressionskoeffizient nicht korrekt schätzen.
Ursachen für Endogenität
Es gibt 3 Ursachen für Endogenität.
- Fehlende (engl. omitted) Variable
Es gibt eine weitere (fehlende) Variable, die mit der erklärenden Variable korreliert, und das beeinflusst auch die abhängige Variable. Das kann gelöst werden, indem diese fehlende Variable in die Regressionsgleichung integriert wird.
Da aber noch andere Faktoren den Stundenlohn der Angestellten beeinflussen, wird der geschätzte Regressionskoeffizient höher sein als der eigentliche Regressionskoeffizient.
Erst, wenn du mögliche fehlende Variablen (wie z. B. das Alter und die Anstellungsdauer der Mitarbeitenden) in dein Regressionsmodell integrierst, erhältst du eine zuverlässige Abschätzung des Stundenlohns.
- Umgekehrte Kausalität
Wenn die abhängige Variable auch die erklärende Variable beeinflusst, dann besteht eine umgekehrte Kausalität.
- Messfehler in der erklärenden Variable
Wenn die erklärende Variable nicht reliabel gemessen wurde, dann ist der Regressionskoeffizient geschätzt näher an 0, als er es tatsächlich ist. Es ist daher wichtig, dass du zuverlässige Daten verwendest.
Vorgehensweise bei Endogenität
Am besten kannst du Endogenität vermeiden, indem du experimentelle Forschung durchführst, in der du die erklärende Variable selbst manipulieren kannst.
Auf Grundlage deiner Daten kannst du nicht sagen, ob womöglich Endogenität besteht. Du kannst allerdings einen kritischen Blick auf dein konzeptuelles Modell werfen.
Schau, ob die Pfeile in die korrekte Richtung zeigen und ob die Variablen vollständig sind, die sowohl deine erklärende, als auch deine abhängige Variable beeinflussen.
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Annahme 5: Homoskedastizität
Die Regressionsgerade verbindet Datenpunkte. Da nicht alle Datenpunkte auf einer Geraden liegen, werden ihre Abweichungen von der Geraden als Störgrößen oder Residuen bezeichnet. Wenn diese Störgrößen alle dieselbe Varianz aufweisen, spricht man von Homoskedastizität oder Varianzhomogenität.
Fehlt diesen Störgrößen dieselbe Varianz, wird eine Regressionsanalyse keine brauchbaren Ergebnisse bringen. Das wird als Heteroskedastizität bezeichnet.
Wenn du einen t-Test oder eine ANOVA durchführst, dann analysierst du die Varianz zwischen mehreren Gruppen. Das Resultat kannst du mit dem Levene’s Test überprüfen.
Heteroskedastizität in der Regression mit SPSS überprüfen
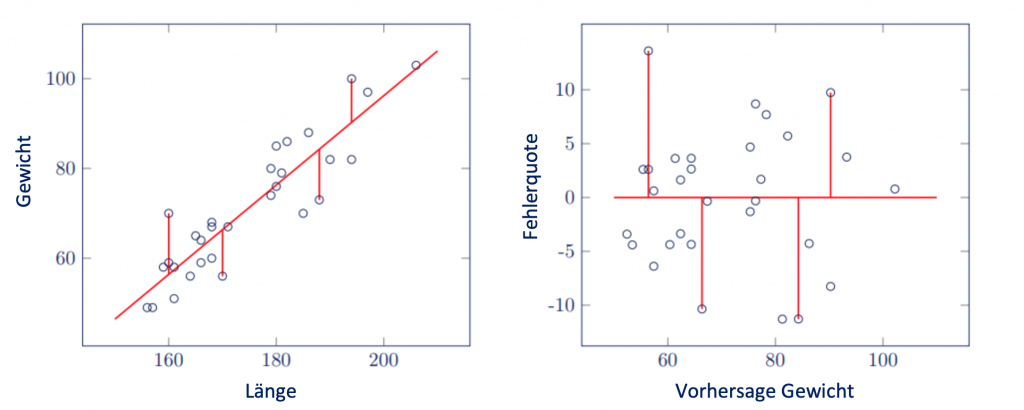
Es ist sinnvoll, ein Streudiagramm zu erstellen, um zu sehen, ob die Varianz der Störgröße gleich ist. In SPSS klickst du auf Speichern, wenn du eine Regression durchführst und markierst Nicht standardisiert unter dem Feld Vorhergesagte Werte und unter dem Feld Residuen.
Das erzeugt zwei neue Variablen, den vorhergesagten Wert und das Residuum. In einem Streudiagramm überträgst du die Variable für das Residuum auf die Y-Achse und die Variable für den vorhergesagten Wert auf die X-Achse.
Die Streudiagramme unten zeigen, dass die Beobachtungen ungefähr dieselbe Distanz zur Regressionslinie für jeden Wert von Größe aufweisen. Es besteht daher keine Heteroskedastizität.
Vorgehensweise bei Heteroskedastizität
Wenn Heteroskedastizität besteht, hast du verschiedene Optionen diese zu verhindern.
- Variablen transformieren
Es ist möglich, dass eine Transformation der Variablen die Heteroskedastizität verschwinden lässt. Heteroskedastizität kann vorkommen, wenn lineare Beziehungen zwischen den erklärenden und abhängigen Variablen nicht bestehen.
Dann ist die erklärende Variable zu transformieren, um eine lineare Beziehung herzustellen, in der sich die Störgröße nicht für höhere oder niedrigere Werte der erklärenden Variable verändert.
- Eine andere Regressionsanalyse verwenden
außer der linearen Regressionsanalyse lässt sich auch eine gewichtete oder generalisierte Regression verwenden. Diese Formen der Regressionsanalysen verlangen keine Homoskedastizität.
Eine logistische Regression lässt sich verwenden, wenn eine Variable nicht intervall- oder ratioskaliert ist.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Flandorfer, P. (2023, 23. Mai). Annahmen für statistische Tests erklärt mit Beispielen. Scribbr. Abgerufen am 21. Oktober 2024, von https://www.scribbr.de/statistik/statistische-tests-annahmen/