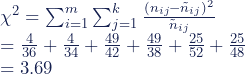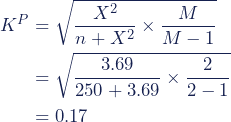Den Kontingenzkoeffizienten bestimmen und interpretieren
Der Kontingenzkoeffizient nach Pearson gibt uns Auskunft über den statistischen Zusammenhang zwischen zwei oder mehreren Variablen.
Am häufigsten wird der Kontingenzkoeffizient für nominal– oder ordinalskalierte Daten verwendet.
Da es sich um ein standardisiertes Maß handelt, ist es möglich, mehrere Variablen hinsichtlich des Kontingenzkoeffizienten zu vergleichen.
Der Kontingenzkoeffizient am Beispiel erklärt
Nehmen wir an, wir wollen den Zusammenhang zwischen der Wahl der Studienrichtung und dem Geschlecht der Studierenden bestimmen.
Dazu befragen wir insgesamt 250 Personen aus drei verschiedenen Studienrichtungen, nämlich Jura, Naturwissenschaften (NW) und Sozialwissenschaften (SW), und erhalten folgende Antworten:
| Jura | NW | SW | Summe (Zeile) | |
|---|---|---|---|---|
| Weiblich | 38 | 35 | 57 | 130 |
| Männlich | 32 | 45 | 43 | 120 |
| Summe (Spalte) | 70 | 80 | 100 | 250 |
Da wir für die Berechnung des Kontingenzkoeffizienten den Chi-Quadrat-Wert benötigen, bestimmen wir diesen zuerst. Den Chi-Quadrat-Wert können wir dann in den Kontingenzkoeffizienten umwandeln.
In unserem Beispiel haben wir ein Chi-Quadrat von χ2 = 3.69.
Genauere Erklärungen zu den einzelnen Berechnungsschritten findest du in unserem Artikel zum Chi-Quadrat.
Vom Chi-Quadrat zum Kontingenzkoeffizienten nach Pearson
Da der Chi-Quadrat-Wert nicht standardisiert und daher nur begrenzt vergleichbar ist, wandeln wir ihn in den Kontingenzkoeffizienten nach Pearson um. Anhand des Kontingenzkoeffizienten können wir dann konkrete Schlüsse und Vergleiche ziehen.
 |
|
 |
Kontingenzkoeffizient nach Pearson |
 |
Chi-Quadrat |
 |
Gesamtanzahl (der Stichprobe) |
 |
 die kleinere der beiden Zahlen für die Zeilenanzahl (  ) und die Spaltenanzahl ( ) |
Für unser Beispiel berechnen wir also Folgendes:
Für M in der Formel zum Kontingenzkoeffizienten nach Pearson setzen wir die kleinere der beiden Anzahlen ein, in unserem Beispiel also 2.
Den Kontingenzkoeffizienten richtig interpretieren
Der Kontingenzkoeffizient kann Werte zwischen 0 und 1 annehmen.
Dabei bedeutet 0, dass es keinen Zusammenhang zwischen den beiden Merkmalen gibt, und 1, dass es einen vollständigen Zusammenhang gibt.
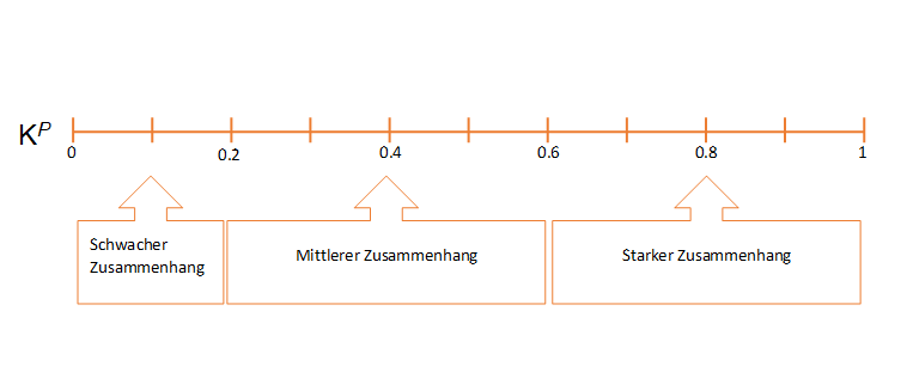
Deinen Kontingenzkoeffizienten kannst du anhand dieser Übersicht interpretieren:
→ kein Zusammenhang
→ vollständiger Zusammenhang
In unserem Beispiel haben wir 
berechnet. Es liegt also ein schwacher statistischer Zusammenhang zwischen den Merkmalen Geschlecht und Wahl der Studienrichtung vor.
Häufig gestellte Fragen
- Was sagt der Kontingenzkoeffizient nach Pearson aus?
-
Der Kontingenzkoeffizient nach Pearson gibt uns Auskunft über den statistischen Zusammenhang zwischen zwei oder mehreren Variablen.
- Was ist der Unterschied zwischen Kontingenzkoeffizient und Chi-Quadrat?
-
Der Kontingenzkoeffizient nach Pearson ist ein standardisiertes Zusammenhangsmaß und lässt daher Vergleiche mehrerer Koeffizienten zu. Chi-Quadrat ist nicht standardisiert und hat daher eine geringere Aussagekraft.
- Wie interpretiere ich den Kontingenzkoeffizienten nach Pearson?
-
Der Kontingenzkoeffizient nach Pearson liegt zwischen 0 und 1. Dabei bedeutet 0, dass es überhaupt keinen Zusammenhang gibt, und 1, dass es einen vollständigen Zusammenhang gibt.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2022, 02. Dezember). Den Kontingenzkoeffizienten bestimmen und interpretieren. Scribbr. Abgerufen am 16. Dezember 2024, von https://www.scribbr.de/statistik/kontingenzkoeffizient/
