Durchführung und Interpretation der Regressionsanalyse
Mit einer Regressionsanalyse überprüfst du, ob ein Zusammenhang zwischen den Werten von zwei oder mehreren Variablen besteht, wie z. B. zwischen dem Gewicht und der Größe einer Person.
Dieser Zusammenhang wird bei einer Regressionsanalyse in Form eines Vergleichs getestet.
Dieser Vergleich zeigt die Veränderung der abhängigen Variable Gewicht, wenn sich der Wert der erklärenden (unabhängigen) Variable Größe um den Wert 1 erhöht.
Inhaltsverzeichnis
- Verwendung der Regressionsanalyse
- Formen von Regressionsanalysen
- Einfache lineare Regressionsanalyse
- Multiple Regressionsanalyse
- Regressionsanalyse mit SPSS, Excel oder Google-Tabellen durchführen
- Regressionsanalyse Interpretation der Ergebnisse
- Regressionsanalyse Zusammenfassung der Ergebnisse
- Statistische Voraussetzungen für die Regressionsanalyse
Verwendung der Regressionsanalyse
Die 3 Hauptgründe für eine Regressionsanalyse sind:
1. Die Stärke des Zusammenhangs zwischen zwei Variablen herausfinden.
- Wie stark ist der Zusammenhang zwischen der Größe und dem Gewicht einer Person?
- Wie stark ist der Zusammenhang zwischen dem Alter und dem Wert eines Autos?
2. Die Veränderung der abhängigen Variablen voraussagen, wenn sich der Wert der erklärenden Variablen verändert.
- Inwiefern verändert sich das Gewicht, wenn sich die Größe einer Person verändert?
- Inwiefern verändert sich der Wert eines Autos, wenn sich das Alter des Autos ändert?
3. Einen zukünftigen Wert voraussagen.
- Wie schwer ist ein 180 cm großer Mann?
- Welchen Wert hat ein Auto, wenn es sechs Jahre alt ist?
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Formen von Regressionsanalysen
Es gibt mehrere Formen der Regressionsanalyse:
- Einfache lineare Regression
- Multiple Regression
- Logistische Regression
Die Form der Regressionsanalyse hängt ab
- von der Anzahl der Variablen, die du testen möchtest und
- vom Skalenniveau der Variablen (Nominal-, Ordinal-, Intervall-, Verhältnisskala).
Bei einer einfachen linearen oder multiplen Regressionsanalyse muss die abhängige Variable intervall- oder verhältnisskaliert sein.
Einfache lineare Regressionsanalyse
Wenn du den Effekt einer erklärenden (oder unabhängigen) Variable auf eine abhängige Variable testen möchtest, verwendest du eine einfache lineare Regressionsanalyse.
Eine einfache lineare Regression kann mit der folgenden Gleichung ausgedrückt werden:
Der Vergleich besteht aus drei Elementen:
– Der Interzept (Achsenabschnitt) ist der Startpunkt der Regressionsanalyse, die sogenannte Konstante. Also gibt es ein Basisgewicht auch, wenn die Größe 0 cm ist.
– Der Regressionskoeffizient zeigt die durchschnittliche Zunahme der abhängigen Variable Gewicht (Y), wenn die erklärende Variable Größe (X) um 1 Zentimeter erhöht wird.
– Der Fehlerwert ist der Teil der abhängigen Variable, der nicht durch die unabhängige Variable erklärt werden kann.
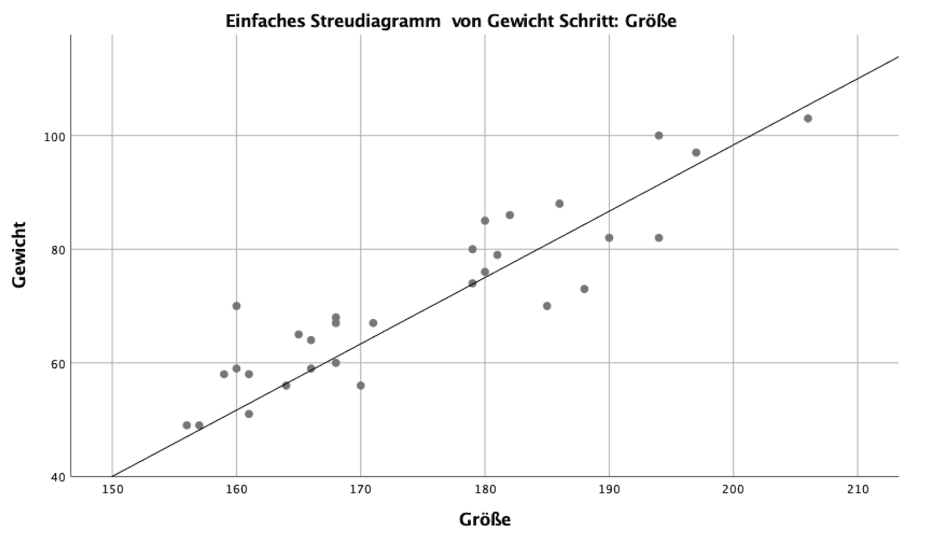
Im Streudiagramm siehst du den linearen Anstieg der Größe bei zunehmendem Gewicht.
Die Linie nennt man Regressionsgerade und sie ergibt sich aus den Datenpunkten der Stichprobe, die um sie gestreut sind.
Multiple Regressionsanalyse
Multiple, oder auch mehrfache Regressionsanalyse genannt, ist eine Erweiterung der einfachen Regression. Dabei werden zwei oder mehrere erklärende Variablen verwendet, um die abhängige Variable (Y) vorhersagen oder erklären zu können.
Du fügst Geschlecht als deine zweite Variable (X2) hinzu.
Daraus ergibt sich diese Regressionsgleichung:
Der einzige Unterschied im Vergleich zur einfachen Regressionsanalyse ist, dass ein zweiter Regressionskoeffizient () für die erklärende Variable Geschlecht hinzugefügt wurde.
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Regressionsanalyse mit SPSS, Excel oder Google-Tabellen durchführen
Regressionsanalysen kannst du mit Programmen wie SPSS, Excel oder Google-Tabellen durchführen.
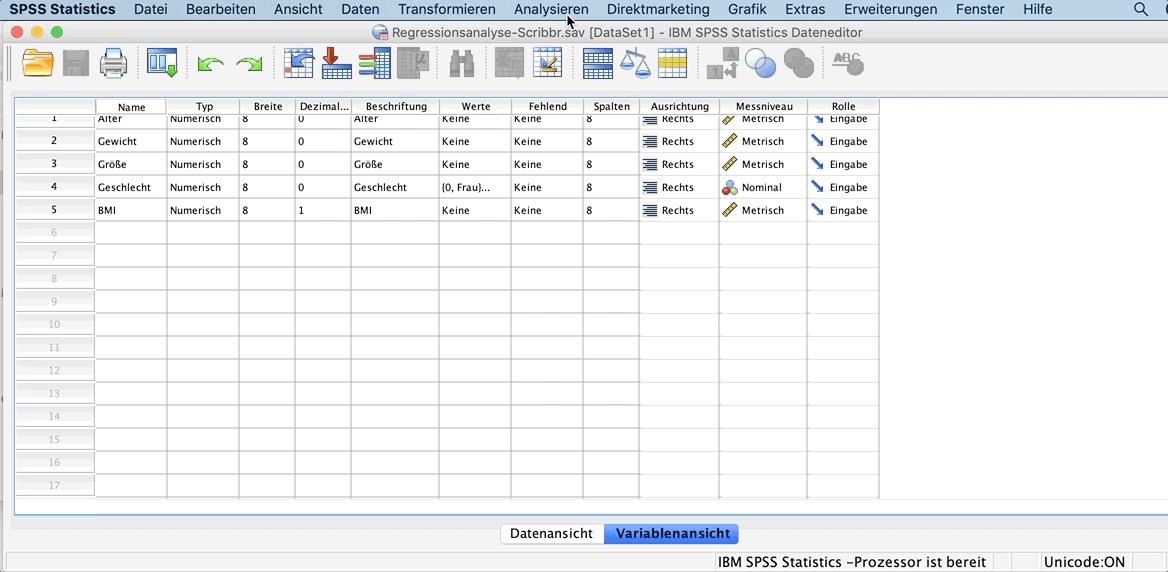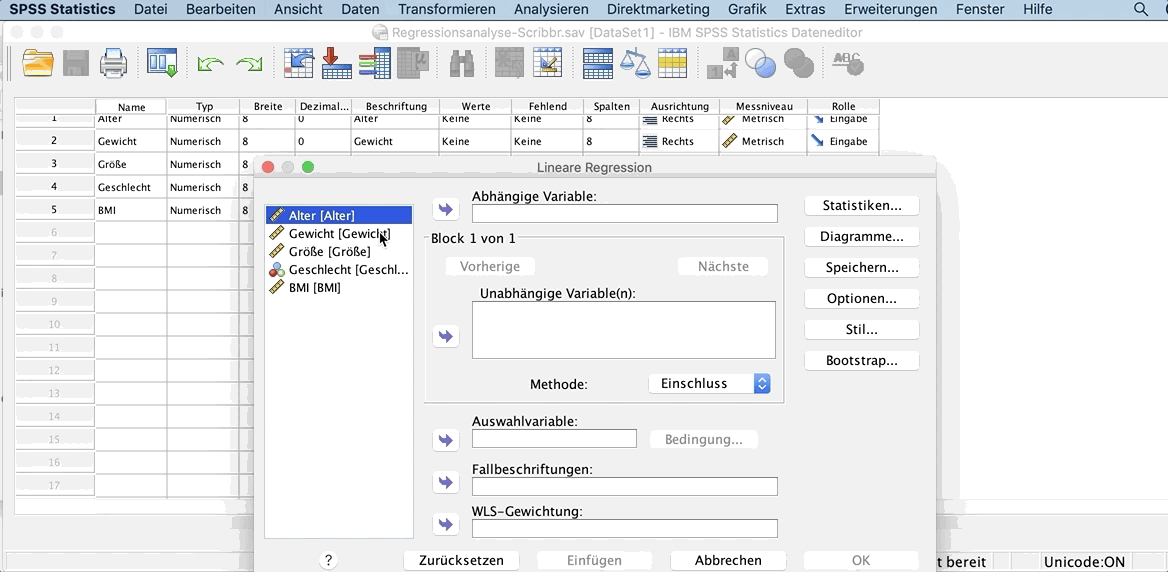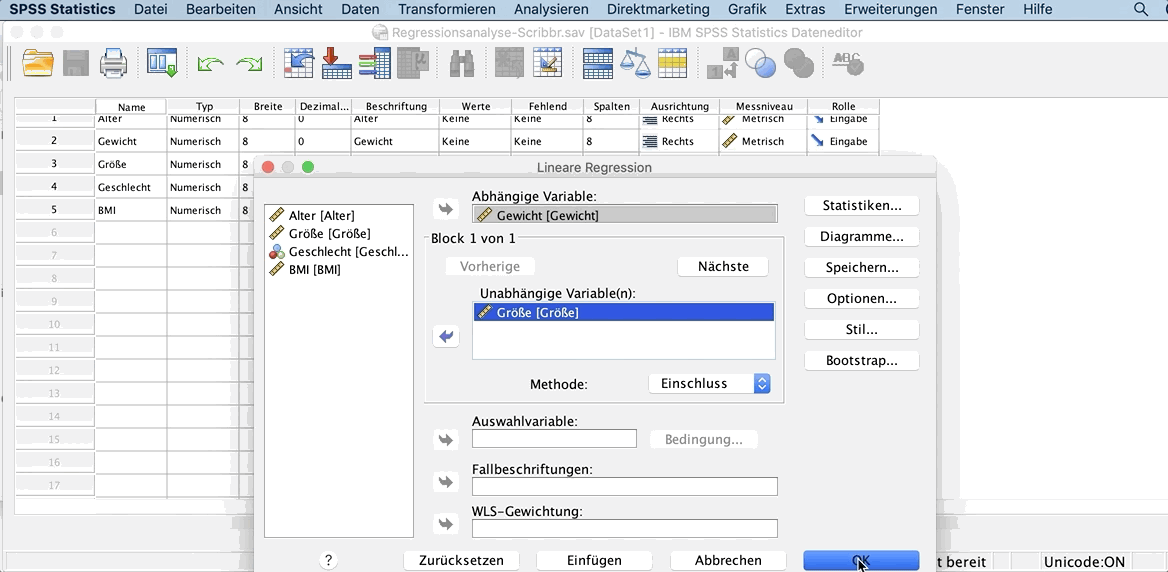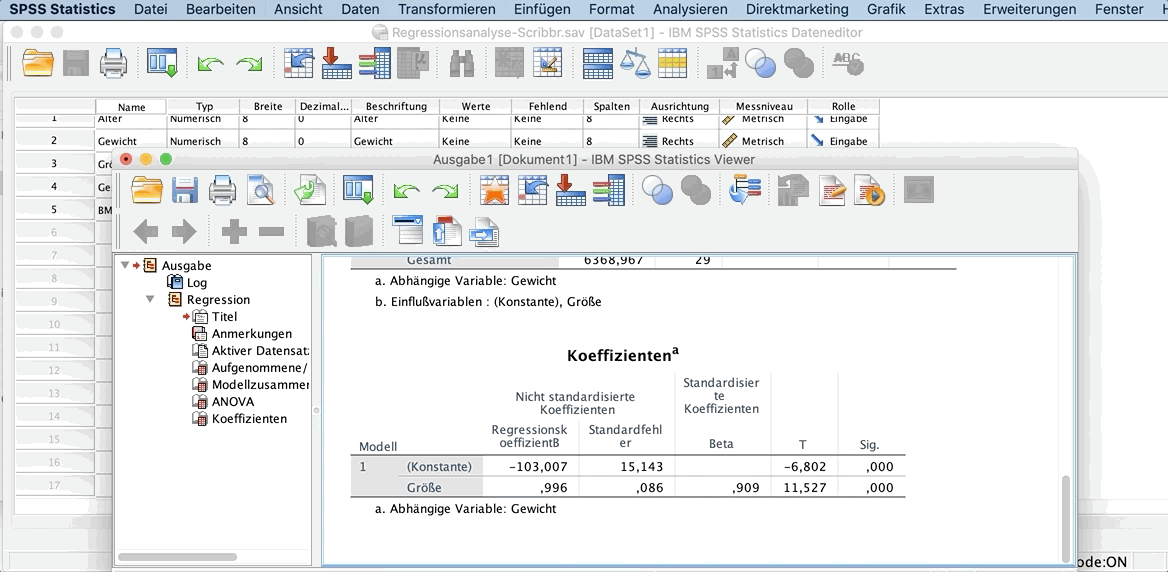
Lade dir unsere SPSS-Datei herunter, um die einfache lineare Regressionsanalyse selbst zu üben. Klicke im Menü auf:
- Analysieren
- Regression
- Linear
In dem geöffneten Fenster verschiebe nun die Variable Gewicht in das Feld Abhängige Variable und die Variable Größe in das Feld Unabhängige Variable(n).
Mit Ok führst du du die Analyse aus.
Lade dir unsere Excel-Datei herunter, um mit denselben Daten zu üben. Für die Analyse mit Excel benötigst du das Analyse Add-In.
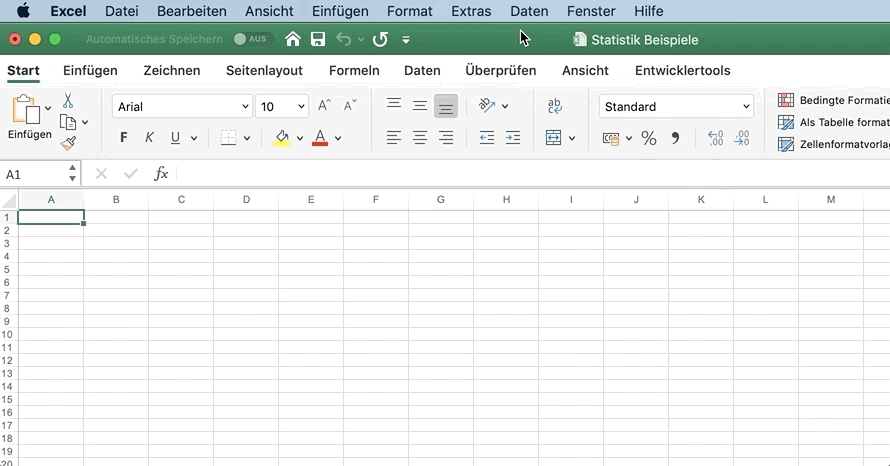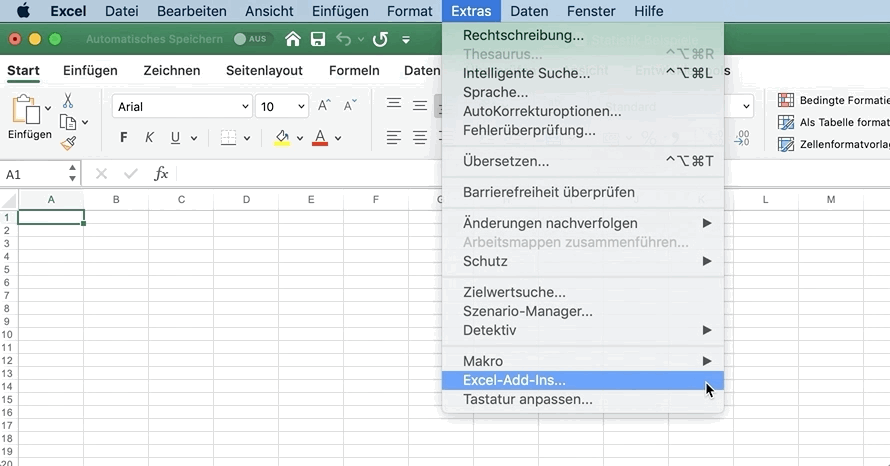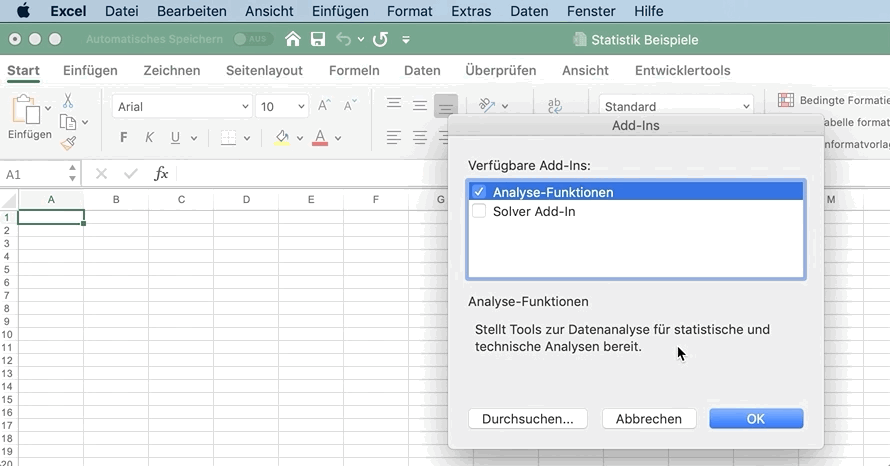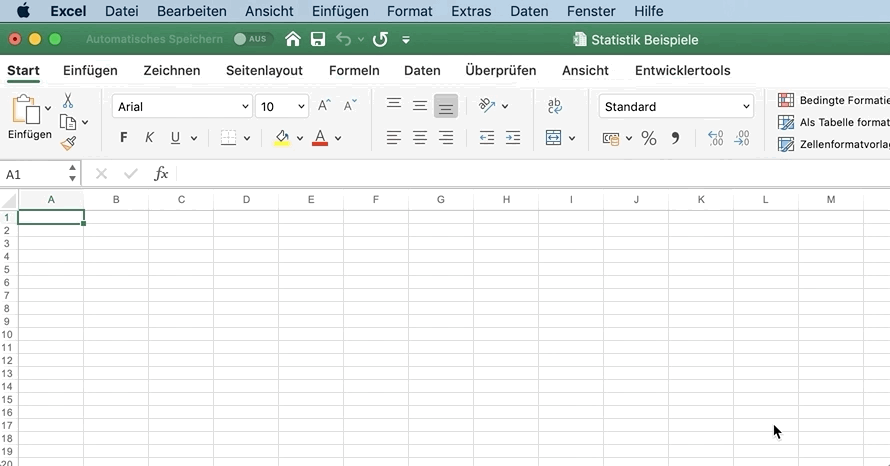
Gehe dafür im Menü auf:
- Extras
- Excel-Add-Ins
- Wähle Analyse-Funktionen aus
Um die Regressionsanalyse durchzuführen, klicke auf:
- Daten
- Datenanalyse (rechtes äußerstes Feld)
- Regression
Input Y Range: Wähle die Daten der abhängigen Variable Y – Gewicht aus (inklusive dem Namen der Spalte).
Input X Range: Wähle die Daten der erklärenden Variable X – Größe aus (inklusive dem Namen der Spalte).
Klicke auf Labels, um anzugeben, dass die oberste Zelle jeweils der Name der Variablen ist.
Unter Output Options wähle New Worksheet Ply. Dadurch werden dir die Ergebnisse in einem neuen Arbeitsblatt angezeigt. Du kannst es Regression nennen.
Klicke auf Ok, um die Analyse durchzuführen.
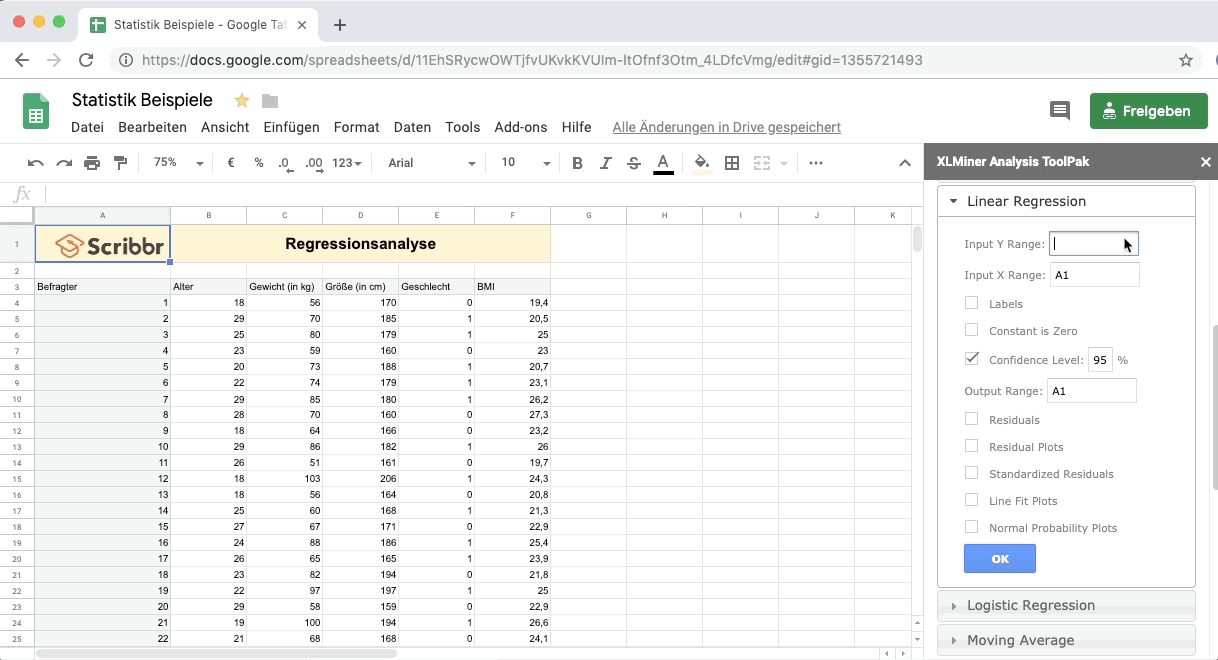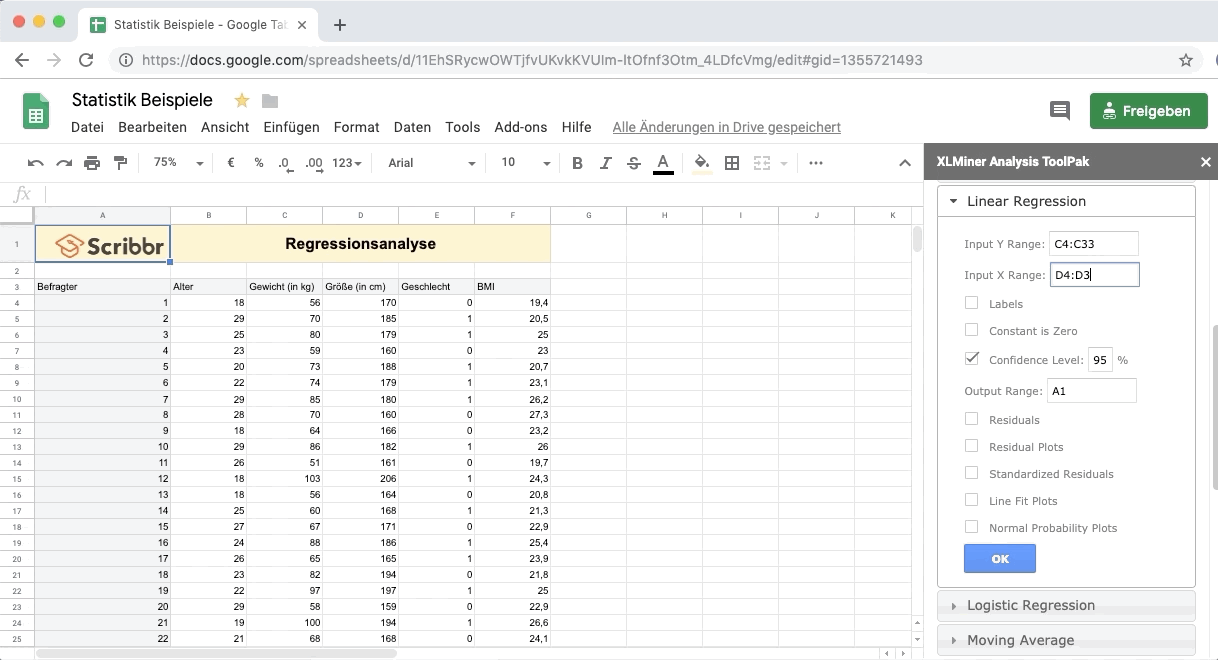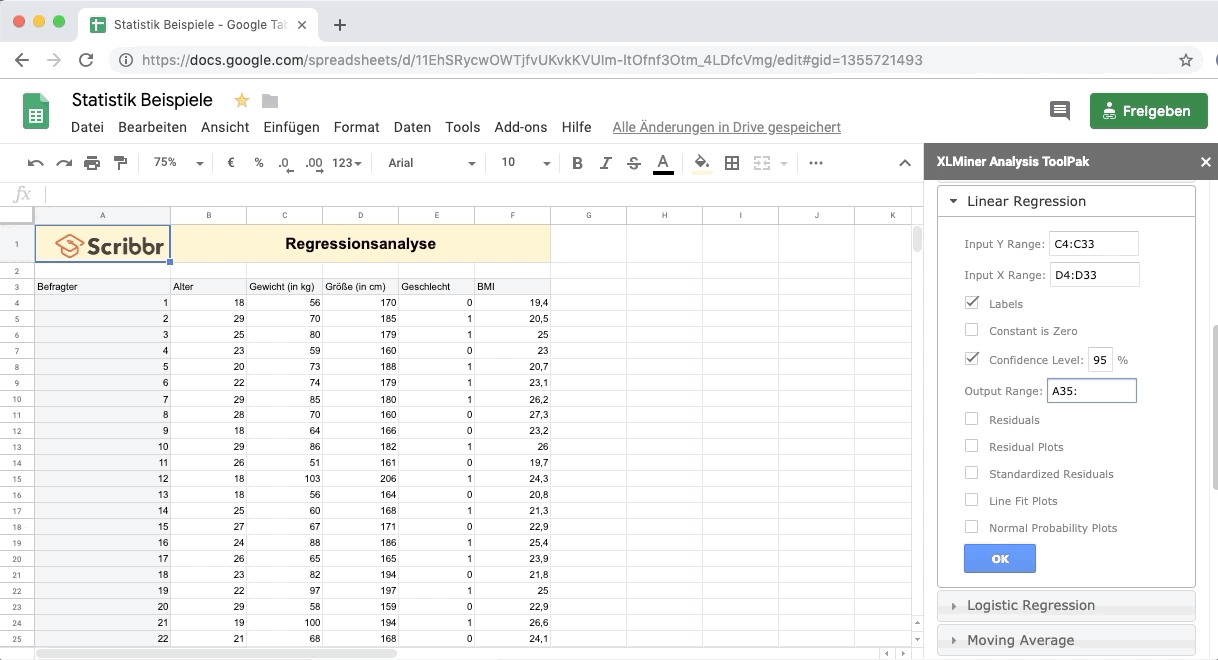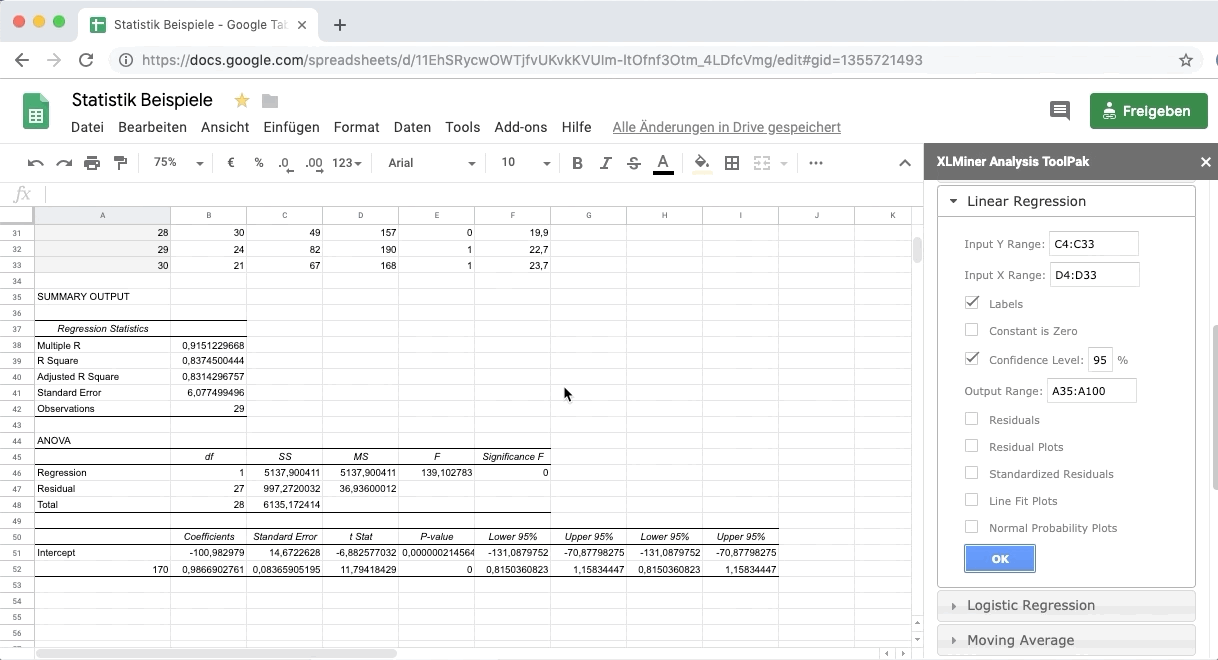
Mit unserer Google-Tabellen Datei kannst du die Regressionsanalyse ausprobieren. Bevor du statistische Berechnungen mit Google-Tabellen durchführen kannst, musst du ein Add-on installieren.
Klicke dafür im Menü auf:
- Add-ons: Add-ons aufrufen
- Suche nach XLMiner Analysis ToolPak und füge es hinzu. Dann klicke wieder auf
- Add-ons und aktiviere das XLMiner Analysis ToolPak.
Um die Regression zu berechnen, wählst du in der Seitenleiste Lineare Regression aus.
Input Y Range: Wähle die Daten der abhängigen Variable Y – Gewicht aus (inklusive dem Namen der Spalte).
Input X Range: Wähle die Daten der erklärenden Variable X – Größe aus (inklusive dem Namen der Spalte).
Klicke auf Labels, um anzugeben, dass die oberste Zelle jeweils dem Namen der Variablen entspricht.
Unter Output Range markiere einen größeren Bereich unter der Tabelle.
Mit Ok erhältst du die Ergebnisse der Regressionsanalyse.
Regressionsanalyse Interpretation der Ergebnisse
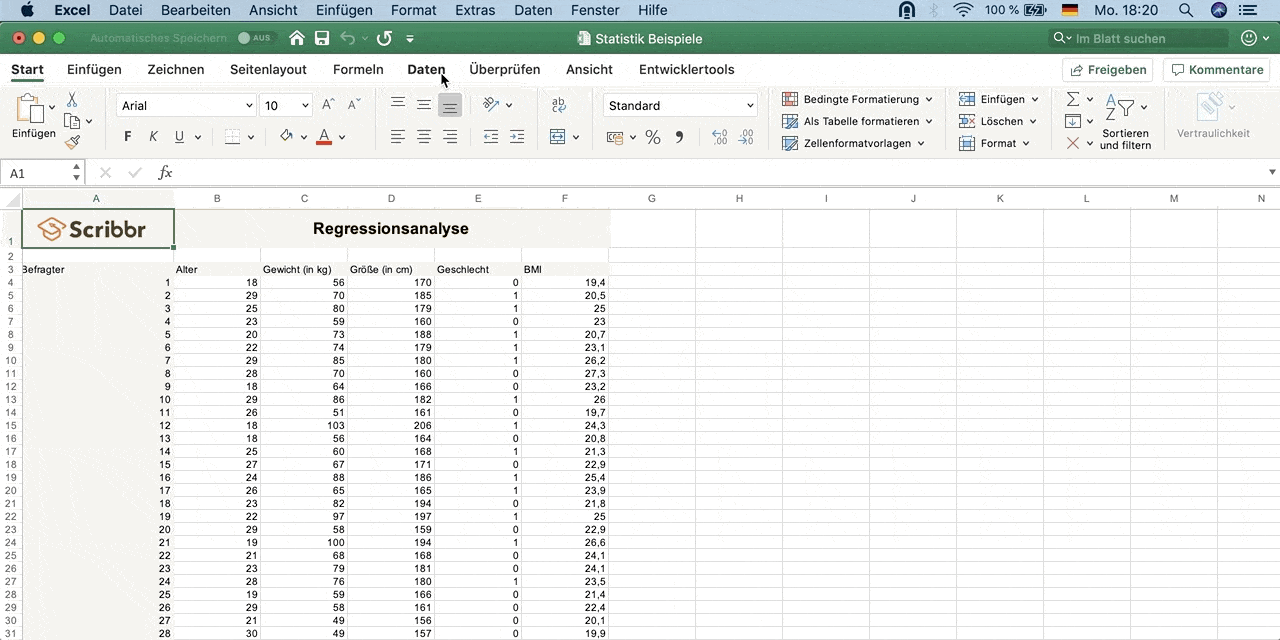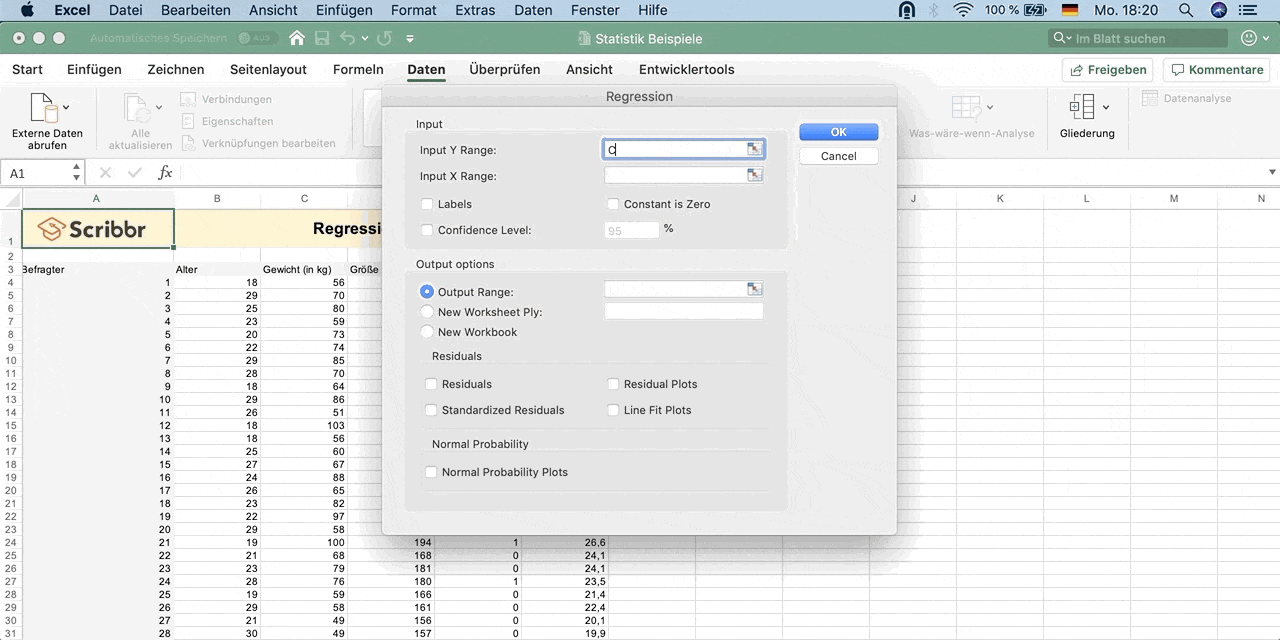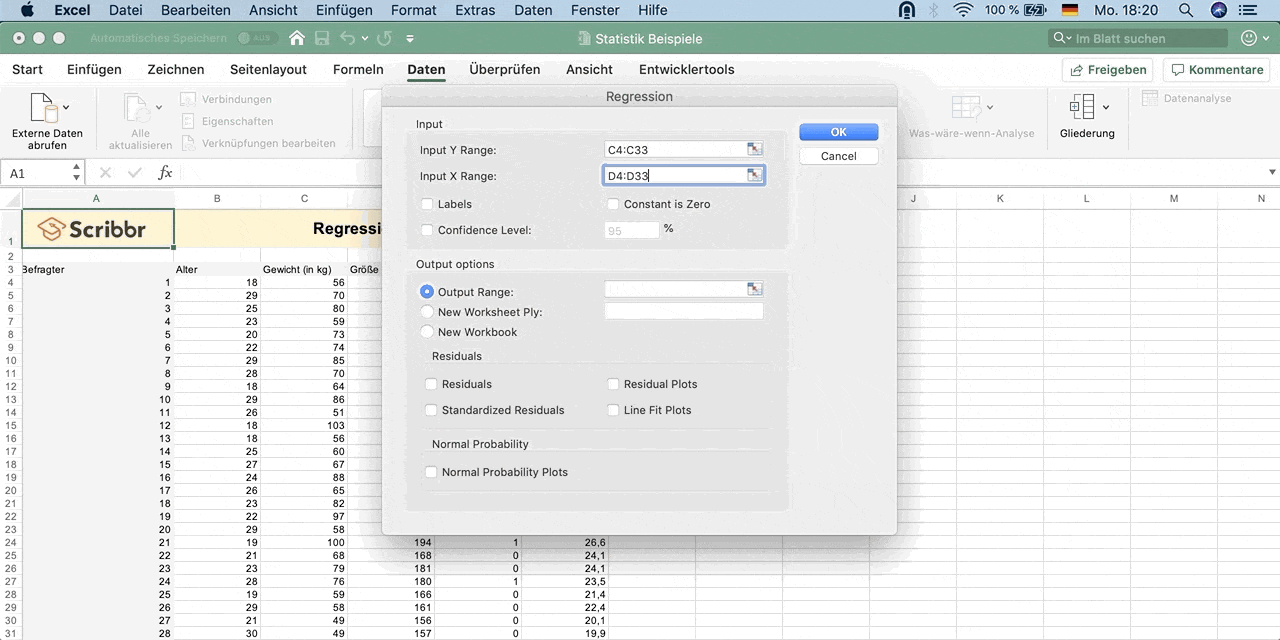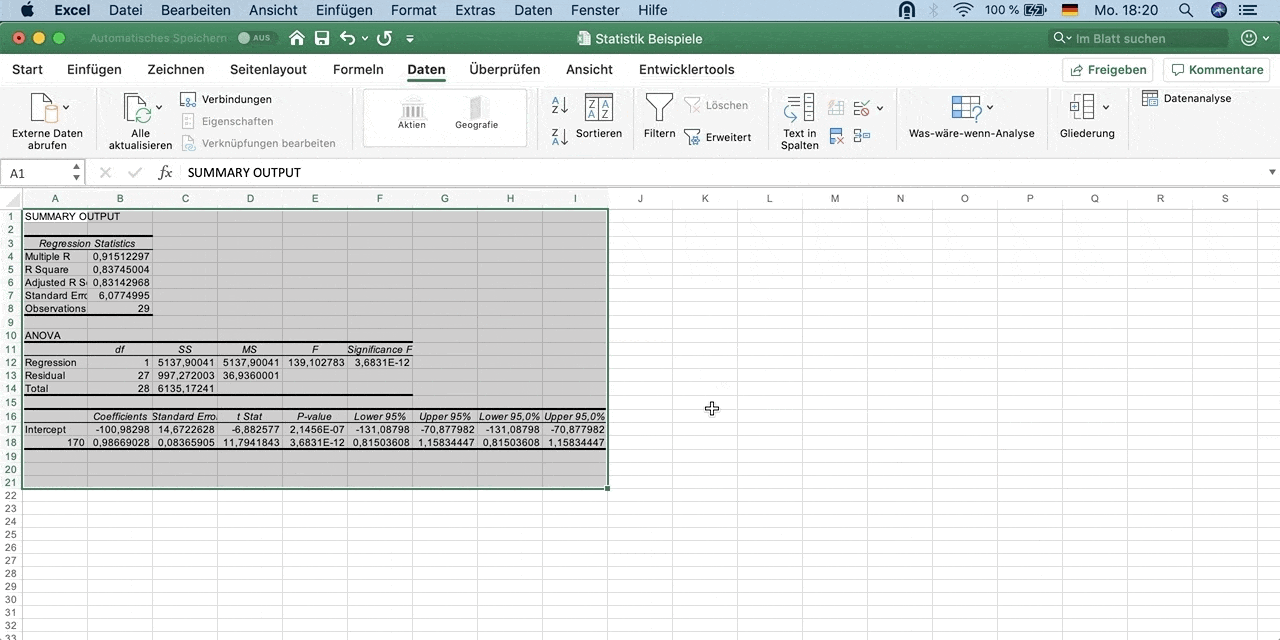
Die Ausgabe einer Regressionsanalyse besteht aus drei Teilen: der Modellzusammenfassung, der ANOVA und den Koeffizienten.
Wir erklären dir die SPSS-Ausgabe für dieses Beispiel. Die Ausgabe von Excel und Google-Tabellen ist sehr ähnlich.
Modellzusammenfassung
Die Modellzusammenfassung zeigt dir mit dem Korrelationskoeffizienten (R) die Stärke des Zusammenhangs und gibt zusätzlich den Wert des Determinationskoeffizienten an.
R: Der Korrelationskoeffizient gibt an, wie hoch der Zusammenhang der beiden Variablen ist.
- Interpretation: Der Korrelationskoeffizient ist mit 0,909 sehr hoch. Es besteht also ein sehr hoher Zusammenhang zwischen Gewicht und Größe.
R-Quadrat: Der Determinationskoeffizient gibt an, wie sehr die Varianz der abhängigen Variable durch die erklärende Variable erklärt wird.
Der Wert dieses Koeffizienten liegt immer zwischen 0 und 1, wobei 1 das beste Modell wäre. Dann würde nämlich die gesamte Varianz der abhängigen Variable durch die unabhängige Variable erklärt werden.
Du kannst den Wert von R-Quadrat mit 100 multiplizieren, um einen Prozent-Wert zu erhalten.
- Interpretation: Ein R-Quadrat von 0,826 bedeutet, dass die Variable Größe 82,6% des Gewichts einer Person erklärt.
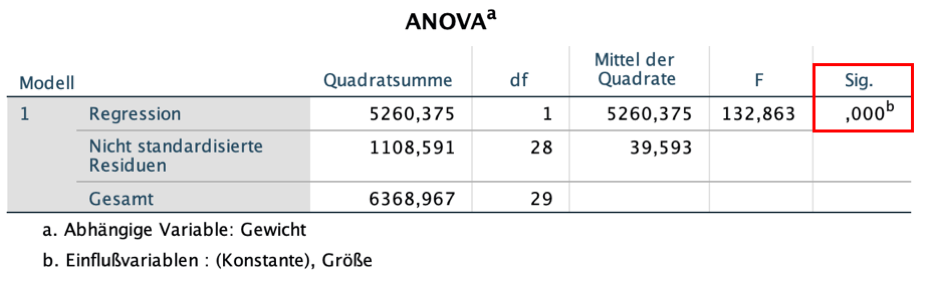
ANOVA
Der zweite Teil der Ausgabe, ANOVA, testet die Signifikanz des Regressionsmodells.
Die Ergebnisse zeigen, wie hoch die Wahrscheinlichkeit ist, dass alle Regressionskoeffizienten tatsächlich 0 sind und das Resultat der Regressionsanalyse daher auf Zufall basiert.
F: F-Test
Um diese Annahme zu testen, wird ein F -Test durchgeführt.
df: Degrees of freedom (Freiheitsgrade)
In den F -Test einbezogen werden Freiheitsgrade:
- df = 1: Anzahl der erklärenden Variablen
- df = 28: Zahl der Beobachtungen (30 Personen) minus der Anzahl der erklärenden Variablen (1) minus 1
Sig.: Signifikanz des Modells
Liegt dieser Wert unter 0,05, dann enthält das Modell signifikante erklärende Variablen.
- Interpretation: Die Wahrscheinlichkeit, einen F -Wert von 132,863 oder größer mit diesen Freiheitsgraden (1,28) zu erhalten, liegt bei 0,000. Das Modell beinhaltet daher signifikante Variablen (Größe).
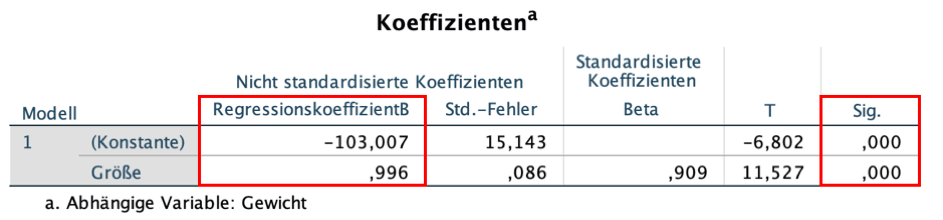
Koeffizienten
Die Tabelle zu den Koeffizienten gibt Auskunft über die Größe, das Vorzeichen der Konstante (plus oder minus) und die Signifikanz des Effekts der erklärenden Variable auf die abhängige Variable.
T und Sig.: t-Test und Signifikanz
Die Signifikanz des Effekts wird mit einem t-Test ermittelt. Ein Ergebnis unter 0,05 ist signifikant.
- Interpretation: Die Wahrscheinlichkeit, einen t-Wert von 11,527 oder größer zu erhalten ist 0,000. Also ist der Effekt signifikant.
Regressionskoeffizient B
Für die Regressionslinie sind die Werte des Regressionskoeffizienten B für die Konstante und die erklärende Variable Größe entscheidend.
Die Regressionslinie folgt der Gleichung:
Gewicht = -103,007 + 0,996 * Größe
- Interpretation: Der geschätzte durchschnittliche Effekt einer Zunahme von einem Zentimeter an Größe ist 996 Gramm (0,996 kg * 1000).
Gewicht = -103,007 + 0,996 * 180 = 76,27 kg
Eine 180 cm große Person ist geschätzt 76,27 kg schwer.
Regressionsanalyse Zusammenfassung der Ergebnisse
Du fasst die Ergebnisse der Regressionsanalyse im Ergebniskapitel deiner Bachelorarbeit oder Masterarbeit zusammen.
Darin hältst du auf jeden Fall fest:
- die erklärte Varianz deines Regressionsmodells (R2 oder R-Quadrat),
- den F -Wert und die Signifikanz deines Regressionsmodells und
- den Regressionskoeffizienten und seine Signifikanz.
Für die Zusammenfassung der Ergebnisse der Regressionsanalyse kannst du die folgenden Sätze verwenden:
Eine einfache lineare Regression mit Gewicht als der abhängigen und Größe als der erklärenden Variable ist signifikant, F (1,28) = 132,86, p < ,001.
82,6% der Varianz von Gewicht kann mit der Variable Größe erklärt werden. Der Regressionskoeffizient der Variable Größe ist 0,996 und ist signifikant (t (28) = 11,53; p < ,001).
Die Größe ist ein signifikanter Prädiktor für Gewicht. Die geschätzte Zunahme an Gewicht ist 996 Gramm pro Zentimeter ( = 0,996; t (28) = 11,53; p < ,001). Die Größe erklärt ebenso einen signifikanten Anteil der Varianz von Gewicht von (R2=, 826; F (1,28) = 132,86, p < ,001).
Statistische Voraussetzungen für die Regressionsanalyse
Damit deine Regressionsanalyse gültige Ergebnisse liefert, müssen einige statistische Voraussetzungen erfüllt sein.
Diese Voraussetzungen werden Gauss-Markov-Annahmen genannt:
- Die Beziehung zwischen der erklärenden und der abhängigen Variable ist linear.
- Die Daten wurden mittels Zufallsstichprobe aus der Grundgesamtheit gezogen.
- Die unabhängigen Variablen, die du in die Regressionsanalyse einschließt, weisen keine lineare Beziehung auf.
- Exogenität: Der erwartete Wert des Fehlers ist 0.
- Homoskedastizität: Die Varianz des Fehlerwertes ist für alle Werte der erklärenden Variablen gleich.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Flandorfer, P. (2023, 20. November). Durchführung und Interpretation der Regressionsanalyse. Scribbr. Abgerufen am 7. Juli 2025, von https://www.scribbr.de/statistik/regressionsanalyse/