Stichprobe – repräsentativ, geschichtet, unabhängig etc
Eine Stichprobe ist eine Teilmenge von Daten aus einer größeren Population (auch Grundgesamtheit genannt), die zur Beantwortung einer Fragestellung untersucht wird.
Wenn du eine Forschungsarbeit über eine Personengruppe durchführst (z. B. Personen, die in der Pflege arbeiten), ist es selten möglich, Daten von jeder Person in dieser Gruppe zu erheben.
Stattdessen wählst du eine Stichprobe aus. Die Stichprobe ist die Gruppe von Personen, die tatsächlich an der Untersuchung teilnehmen (z. B. 500 Personen, die in der Pflege arbeiten).
Inhaltsverzeichnis
- Grundgesamtheit vs. Stichprobe
- Unabhängige Stichprobe vs. abhängige Stichprobe
- Eine repräsentative Stichprobe ziehen
- Zufallsstichproben ziehen: 3 Methoden
- Nichtprobablistische Stichproben ziehen: 4 Methoden
- Grundgesamtheit N und Stichprobe n
- Gesamtstichprobe N und Teilstichprobe n
- Häufig gestellte Fragen
Grundgesamtheit vs. Stichprobe
Die Grundgesamtheit ist die gesamte Gruppe, über die du Schlussfolgerungen ziehen willst.
Die Stichprobe ist die spezifische Gruppe von Personen, von der du Daten erhebst.
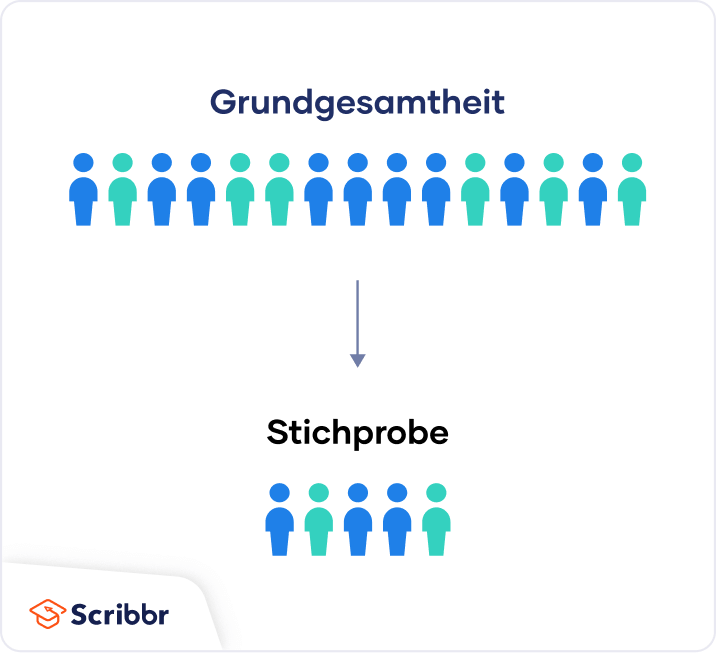
Stichprobe: 150 Personen, die ein Ehrenamt ausüben.
Die Grundgesamtheit kann anhand verschiedener Merkmale definiert werden, z. B. anhand des geografischen Standorts, des Alters, des Einkommens und vielen anderer Merkmale.
Sie kann breit oder eng gefasst sein:
- Breit: Du willst Rückschlüsse auf die gesamte erwachsene Bevölkerung eines Landes ziehen.
- Eng: Du untersuchst Kundinnen eines bestimmten Unternehmens oder Personen mit einem bestimmten Gesundheitszustand.
Erhebungsrahmen (auch: Stichprobenrahmen)
Der Erhebungsrahmen ist die Liste der Personen, aus der die Stichprobe gezogen werden soll.
Im Idealfall sollte der Erhebungsrahmen die gesamte Grundgesamtheit umfassen und niemanden, der nicht zur Grundgesamtheit gehört.
Deine Grundgesamtheit sind alle 1000 Mitarbeitenden des Krankenhauses.
Dein Erhebungsrahmen ist die Personaldatenbank des Krankenhauses, in der die Namen und Kontaktinformationen aller 1000 Mitarbeitenden aufgeführt sind.
Stichprobengröße
Die Stichprobengröße ist die Anzahl der Elemente oder Individuen in einer Stichprobe, die aus einer größeren Grundgesamtheit gezogen wird, um statistische Erkenntnisse über die Grundgesamtheit zu erhalten.
Wie viele Personen du in deine Stichprobe aufnehmen solltest, hängt von verschiedenen Faktoren ab, zum Beispiel von
- der Größe der Grundgesamtheit,
- den Streuungsmaßen der Grundgesamtheit und
- deinem Forschungsdesign.
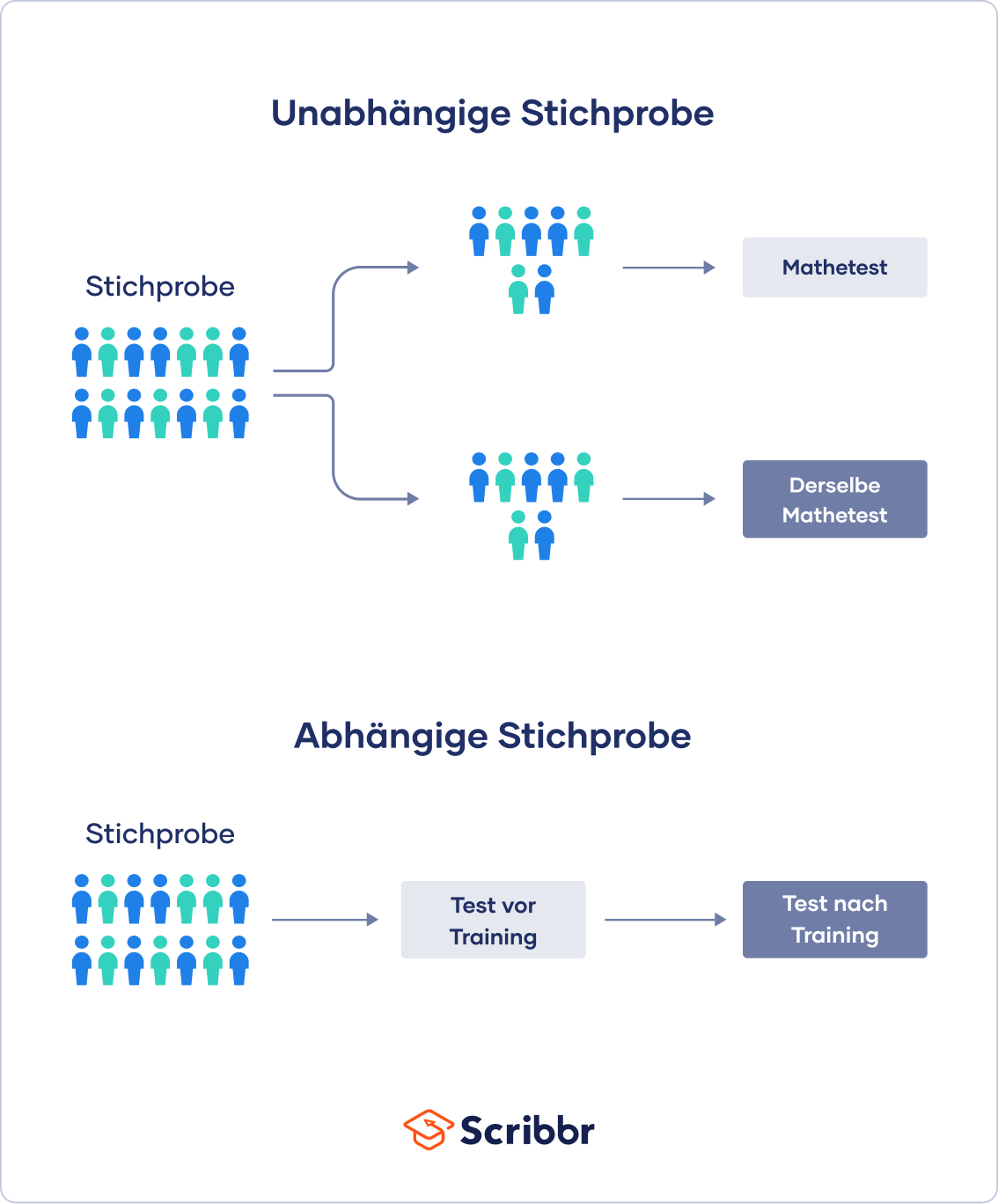
Unabhängige Stichprobe vs. abhängige Stichprobe
Unabhängige Stichproben sind Stichproben, zwischen denen keine Beziehung besteht und die sich nicht gegenseitig beeinflussen.
Die beiden Gruppen haben keine Beziehung zueinander und die Ergebnisse in der einen Gruppe haben keine Auswirkungen auf die Ergebnisse in der anderen Gruppe.
Abhängige Stichproben sind Stichproben, zwischen denen eine Beziehung besteht.
Am Ende des Trainings wird die Herzfrequenz derselben Gruppe erneut gemessen, um festzustellen, ob das Trainingsprogramm tatsächlich eine Verbesserung der Fitness bewirkt hat.
In diesem Fall hängen die Messungen der Teilnehmenden voneinander ab und die Ergebnisse für jede teilnehmende Person sind miteinander verbunden.
Eine repräsentative Stichprobe ziehen
Eine repräsentative Stichprobe ist eine Stichprobe, die für die Grundgesamtheit repräsentativ ist.
Nur wenn deine Stichprobe repräsentativ ist, sind die Ergebnisse deiner Untersuchung valide.
Der Prozess, eine solche Stichprobe zu finden, wird Stichprobenverfahren oder Sampling-Methode genannt.
Es gibt zwei Haupttypen von Stichprobenverfahren, die du in deiner Untersuchung verwenden kannst:
Im Methodikteil deiner Arbeit solltest du klar darlegen, wie du deine Stichprobe ausgewählt hast und warum du dich für eine bestimmte Stichprobe entschieden hast.
Zufallsstichproben ziehen: 3 Methoden
Eine Zufallsstichprobe ist eine Stichprobe, bei der jede Person der Grundgesamtheit eine Chance hat, ausgewählt zu werden.
Zufallsstichproben werden vor allem in der quantitativen Forschung eingesetzt.
Zufallsstichproben sind die beste Wahl, wenn du Ergebnisse erhalten willst, die für die gesamte Grundgesamtheit repräsentativ sind.
Es gibt drei Hauptmethoden zur Erhebung von Zufallsstichproben.
I Einfache Zufallsstichprobe
Bei einer einfachen Zufallsstichprobe hat jede Person in einer Grundgesamtheit die gleiche Chance, ausgewählt zu werden.
Dein Erhebungsrahmen umfasst die gesamte Grundgesamtheit.
Um eine einfache Zufallsstichprobe zu ziehen, kannst du Hilfsmittel wie Zufallszahlengeneratoren verwenden.
Dazu weist du jeder mitarbeitenden Person eine Nummer von 1 bis 1000 zu und verwendest einen Zufallszahlengenerator, um 100 Nummern auszuwählen.
II Geschichtete Zufallsstichprobe
Bei der geschichteten Stichprobe werden die Personen in der Grundgesamtheit auf der Grundlage verschiedener Merkmale in Untergruppen (sogenannte Schichten) unterteilt.
Mögliche Merkmale sind:
- Geschlechtsidentität
- Altersgruppe
- Einkommensgruppe
- berufliche Funktion
Auf Grundlage der Gesamtverteilung der Grundgesamtheit wird berechnet, wie viele Personen aus jeder Untergruppe in die Stichprobe aufgenommen werden sollten.
Anschließend ziehst du zufällig aus jeder der Untergruppen die notwendige Anzahl an Personen, um eine repräsentative Stichprobe zu erhalten.
Die Unterteilung in Untergruppen ermöglicht genauere Schlussfolgerungen, da sichergestellt wird, dass jede Untergruppe in der Stichprobe angemessen vertreten ist.
Deine Stichprobe soll 100 Personen umfassen.
Um sicherzustellen, dass die Stichprobe das Geschlechtergleichgewicht im Unternehmen widerspiegelt, teilst du die Grundgesamtheit nach Geschlecht in zwei Schichten ein.
Dann ziehst du aus jeder der beiden Gruppen eine Zufallsstichprobe:
- Aus der weiblichen Gruppe ziehst du 80 Frauen
- Aus der männlichen Gruppe ziehst du 20 Männer
III Klumpenstichprobe
Bei der Klumpenstichprobe wird die Grundgesamtheit ebenfalls in Untergruppen unterteilt, aber jede Untergruppe sollte ähnliche Merkmale wie die gesamte Stichprobe aufweisen.
Anstatt anschließend einzelne Personen aus jeder Untergruppe auszuwählen, wählst du ganze Untergruppen nach dem Zufallsprinzip aus.
Diese Methode eignet sich gut für große Grundgesamtheiten und solche mit weiten Streuungsmaßen.
Sie birgt jedoch ein höheres Fehlerrisiko, da es erhebliche Unterschiede zwischen den Untergruppen geben kann (Klumpeneffekt).
Es ist schwer zu garantieren, dass die Untergruppen wirklich repräsentativ für die Grundgesamtheit sind.
Da du nicht die Möglichkeit hast, alle zehn Abteilungen zu untersuchen, wählst du mithilfe einer Zufallsstichprobe 3 Büros aus. Das sind deine Untergruppen.
Nichtprobablistische Stichproben ziehen: 4 Methoden
Eine nichtprobablistische Stichprobe ist eine Stichprobe, bei der die Personen nicht nach zufälligen Kriterien ausgewählt werden. Deshalb hat nicht jede Person dieselbe Chance, ausgewählt zu werden.
Diese Art von Stichprobe ist einfacher und billiger zu erhalten, birgt aber ein höheres Risiko der Stichprobenverzerrung.
Daher sind die Rückschlüsse, die du von der Stichprobe auf die Grundgesamtheit ziehen kannst, tendenziell schwächer als bei Zufallsstichproben.
Nichtprobablistische Stichproben werden häufig in der qualitativen Forschung und in der explorativen Forschung verwendet.
Bei diesen Forschungsarten besteht das Ziel nicht darin, eine Hypothese über eine Grundgesamtheit zu überprüfen. Stattdessen soll ein erstes Verständnis für eine kleine oder bisher wenig erforschte Population entwickelt werden.
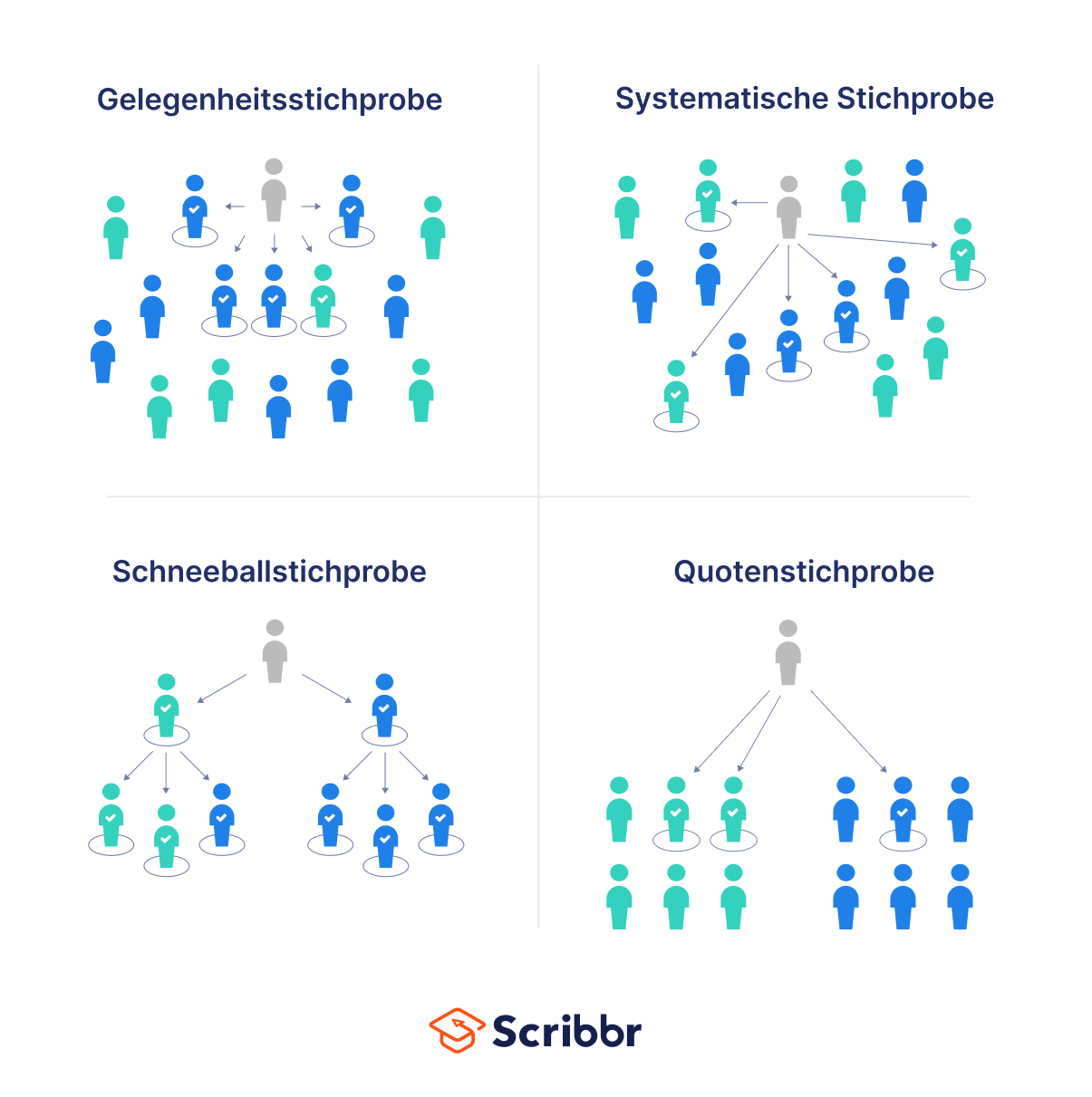
Es gibt vier Hauptmethoden zur Erhebung von nichtprobabilistischen Stichproben
I Gelegenheitsstichprobe
Eine Gelegenheitsstichprobe ist eine Stichprobe, bei der die untersuchten Personen aufgrund ihrer leichten Verfügbarkeit oder Zugänglichkeit ausgewählt werden, anstatt zufällig ausgewählt zu werden.
Eine Gelegenheitsstichprobe ist ein einfacher und kostengünstiger Weg, um erste Daten zu sammeln.
Allerdings gibt es keine Möglichkeit, um festzustellen, ob die Stichprobe repräsentativ für die Grundgesamtheit ist, sodass sie keine verallgemeinerbaren Ergebnisse liefern kann.
Bei Zufallsstichproben besteht die Gefahr einer Stichprobenverzerrung und einer Auswahlverzerrung.
Dazu bittest du deine Kommilitoninnen und Kommilitonen nach jeder Vorlesung, die du besuchst, eine Umfrage zu diesem Thema auszufüllen.
Das ist zwar bequem, aber da du nur Studierende befragst, die die gleichen Veranstaltungen belegen wie du, ist die Stichprobe nicht repräsentativ für alle Studierenden an deiner Universität.
II Systematische Stichprobe
Eine systematische Stichprobe ist eine Stichprobe, bei der die forschende Person die untersuchten Personen mithilfe ihres Fachwissens auswählt.
Sie wird häufig in der qualitativen Forschung eingesetzt, wenn
- die forschende Person detaillierte Kenntnisse über ein bestimmtes Phänomen gewinnen möchte, anstatt statistische Schlüsse zu ziehen, oder
- die Grundgesamtheit sehr klein und spezifisch ist.
Damit die systematische Stichprobe aussagekräftig ist, muss es klare Ein- und Ausschlusskriterien geben, die die forschende Person auch hinreichend erläuterst.
Dazu wählst du eine Reihe von Studierenden mit unterschiedlichem Unterstützungsbedarf aus, um ein breites Spektrum an Daten über ihre Erfahrungen zu sammeln.
III Schneeballstichprobe
Die Schneeballstichprobe ist eine Stichprobe, bei der Teilnehmende durch Empfehlungen anderer Teilnehmenden rekrutiert werden, um eine spezifische Grundgesamtheit zu untersuchen.
Der Vorteil der Schneeballstichprobe ist, dass du auch für eine schwer zugängliche Grundgesamtheit eine Stichprobe ziehen kannst.
Der Nachteil ist, dass du nicht wissen kannst, wie repräsentativ die Stichprobe ist, da du darauf angewiesen bist, dass die Teilnehmenden andere Teilnehmende rekrutieren.
Das kann zu Stichprobenverzerrungen führen.
Da es keine Liste aller Obdachlosen in der Stadt gibt, ist es nicht möglich, eine Wahrscheinlichkeitsstichprobe zu ziehen.
Stattdessen suchst du eine obdachlose Person, die sich bereit erklärt, an der Untersuchung teilzunehmen. Diese Person bringt dich mit anderen obdachlosen Personen in Kontakt, die sie kennt.
IV Quotenstichprobe
Eine Quotenstichprobe ist eine Stichprobe, bei der Teilnehmende nach vorher festgelegten Quoten so ausgewählt werden, dass sie repräsentativ für die Grundgesamtheit sind.
Die Quoten können beispielsweise nach Alter, Geschlecht oder Bildungsgrad festgelegt werden.
Quotenstichproben werden häufig verwendet, wenn eine einfache Zufallsstichprobe nicht ausreichend repräsentativ wäre.
Da es keine umfassende Liste aller Bürger/-innen gibt, entscheidest du dich für eine Quotenstichprobe, um eine repräsentative Stichprobe zu erhalten.
Um sicherzustellen, dass alle Altersgruppen vertreten sind, legst du fest, dass die Stichprobe wie folgt nach Altersgruppen aufgeteilt sein soll:
- 20 % aus der Altersgruppe der 18–29-Jährigen
- 30 % aus der Gruppe der 30–49-Jährigen
- 30 % aus der Gruppe der 50–64-Jährigen
- 20 % aus der Gruppe der 65-Jährigen und älteren Menschen
Außerdem soll die Stichprobe zu 45 % aus Frauen, zu 45 % aus Männern und zu 10 % aus diversen Personen bestehen.
Grundgesamtheit N und Stichprobe n
Je nachdem, ob es sich um eine Grundgesamtheit oder Stichprobe handelt, verwenden wir unterschiedliche Zeichen und Buchstaben.
- N für Grundgesamtheit, n für Stichprobe
Verwende ein großgeschriebenes N, wenn du die Gesamtanzahl einer Grundgesamtheit angeben willst, und einen Kleinbuchstaben (n) für die Größe der Stichprobe.
- Griechische Buchstaben für Grundgesamtheit
Ob es bei einer Formel um die Berechnung von Parametern einer Grundgesamtheit oder einer Stichprobe geht, kannst du dir mit einer Eselsbrücke leicht merken: Sind in der Formel griechische Buchstaben, geht es um Parameter der Grundgesamtheit, bei lateinischen Buchstaben geht es um die Stichprobe.
Die unterschiedliche Verwendung der Buchstaben kannst du beispielsweise bei den beiden Formeln zur Bestimmung der Varianz sehen.
Gesamtstichprobe N und Teilstichprobe n
Nach APA wird das großgeschriebene N für die Gesamtstichprobe verwendet und das kleingeschriebene n für Teilstichproben.
Die 60 Person werden in zwei unterschiedlich große Gruppen – einmal 40 Personen und einmal 20 Personen – unterteilt. Daher ist n1 = 40 und n2 = 20.
- N kann also sowohl für die Grundgesamtheit als auch für die Gesamtstichprobe stehen.
- n kann sowohl für die Gesamtstichprobe als auch für einen Teil der Stichprobe stehen.
Häufig gestellte Fragen
- Welche Arten von Stichproben gibt es?
-
Um welche Stichprobe es sich handelt, hängt davon ab, wie sie bestimmt wurde. Generell unterscheiden wir Zufallsstichproben und nichtprobabilistische Stichproben.
- Was ist der Unterschied zwischen N und n?
-
Allgemein steht der Großbuchstabe N für die Gesamtanzahl der Grundgesamtheit und der Kleinbuchstabe n für die Größe der Stichprobe.
Nach APA wird das großgeschriebene N jedoch auch für die Gesamtstichprobe verwendet und das kleingeschriebene n für Teilstichproben.
- Was ist eine repräsentative Stichprobe?
-
Eine repräsentative Stichprobe erlaubt es, basierend auf den Ergebnissen der Stichprobe Aussagen über die zugrundeliegende Grundgesamtheit zu treffen.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Solis, T. (2020, 12. Mai). Stichprobe – repräsentativ, geschichtet, unabhängig etc. Scribbr. Abgerufen am 18. November 2024, von https://www.scribbr.de/statistik/stichprobe/
