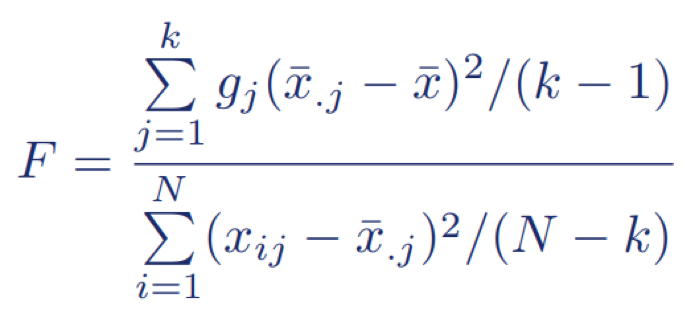ANOVA - Varianzanalyse durchführen und interpretieren
ANOVA steht für Varianzanalyse (engl. Analysis of Variance) und wird verwendet um die Mittelwerte von mehr als 2 Gruppen zu vergleichen.
Sie ist eine Erweiterung des t-Tests, der die Mittelwerte von maximal 2 Gruppen vergleicht.
Formen der Varianzanalyse
Es gibt unterschiedliche Formen der Varianzanalyse. Welche du verwendest, hängt von deinen Daten und deinem konzeptionellen Modell ab. Am häufigsten werden die einfaktorielle und die zweifaktorielle Varianzanalyse angewendet.
Einfaktorielle Varianzanalyse
Du verwendest die einfaktorielle Varianzanalyse, wenn du eine Gruppenvariable für alle Gruppen hast sowie eine abhängige Variable.
Zweifaktorielle Varianzanalyse
Die zweifaktorielle Varianzanalyse verwendest du, wenn 2 oder mehr Gruppenvariablen in deinem konzeptionellen Modell zusammen mit einer abhängigen Variable vorhanden sind.
Mehrfaktorielle Varianzanalyse (MANOVA)
Die mehrfaktorielle Varianzanalyse wendest du an, wenn es mehrere abhängige Variablen gibt. Du kannst diese ANOVA jeweils mit einer oder mehreren Gruppenvariablen durchführen.
Du könntest natürlich mehrere individuelle ANOVAs durchführen. Dann steigt aber die Wahrscheinlichkeit für einen Fehler 1. Art oder α-Fehler, also die inkorrekte Annahme dass es Unterschiede zwischen den Gruppen gibt.
Verwende daher immer eine MANOVA, wenn du mehrere abhängige Variablen hast.
ANOVA mit Messwiederholungen
Wenn du eine Gruppe von Befragten zu mehreren Zeitpunkten untersuchen möchtest, verwendest du eine ANOVA mit Messwiederholungen.
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
ANOVA mit SPSS, Excel oder Google-Tabellen durchführen
Du kannst die Programme SPSS, Excel und Google-Tabellen verwenden, um eine Varianzanalyse (ANOVA) durchzuführen.
Wir zeigen dir die Vorgehensweise für die einfaktorielle und zweifaktorielle ANOVA.
Die Vorgehensweisen für eine MANOVA mit Messwiederholung ähneln großenteils denen für eine ANOVA.
ANOVA mit SPSS
Lade dir unsere SPSS Datei herunter, um mit denselben Daten zu üben.
Um die einfaktorielle Varianzanalyse durchzuführen, klicke im SPSS-Menü auf:
- Analysieren
- Mittelwerte vergleichen
- Einfaktorielle Varianzanalyse
Im geöffneten Fenster füge die Variable Größe als abhängige Variable und die Variable Sport als Faktor hinzu.
Unter Optionen kannst du Deskriptive Statistik auswählen, um auch die Mittelwerte der Gruppen zu erhalten.
Es ist sinnvoll zu testen, ob die Bedingung für gleiche Varianzen (Homoskedastizität) erfüllt ist.
Klicke dafür auf Test auf Homogenität der Varianzen. Mit Weiter und OK führst du die Analyse durch.
Einfaktorielle Varianzanalyse in SPSS
Um die zweifaktorielle Varianzanalyse mit SPSS durchzuführen, klicke im Menü auf:
- Analysieren
- Allgemeines Lineares Modell
- Univariat (oder wähle Multivariat oder Messwiederholung)
Im geöffneten Fenster wähle die Variable Größe im Feld Abhängige Variable und im Feld Feste Faktoren trägst du die Variablen Geschlecht und Sport ein.
Unter Geschätzte Randmittel in den Optionen kannst du (Unter-)Gruppen bei Mittelwerte anzeigen für einfügen, wenn du die Mittelwerte wissen möchtest.
Klicke auf OK, um die Analyse durchzuführen.
Zweifaktorielle Varianzanalyse in SPSS
ANOVA mit Excel
Mit unserer Excel-Datei kannst du gleich selbst die Varianzanalysen ausprobieren.
Für die Berechnung der einfaktoriellen Varianzanalyse mit Excel klicke im Menü auf:
- Extras
- Datenanalyse
- ANOVA: Single Factor (einfaktorielle Varianzanalyse)
Unter Input Range wählst du die Daten für alle drei Sportarten inklusive der Labels aus.
Markiere Labels in first row.
Für Output Range klicke in ein Feld neben den Daten. Dort werden die Ergebnisse der ANOVA ausgegeben.
Mit OK führst du die Analyse aus.
Einfaktorielle Varianzanalyse in Excel
Um die zweifaktorielle Varianzanalyse mit Excel durchzuführen klicke im Menü auf:
- Extras
- Datenanalyse
- ANOVA: Two-Factor With Replication (zweifaktorielle Varianzanalyse)
Für das Feld Input Range markierst du alle Daten mitsamt den Labels.
Bei Rows per sample gibst du die Zahl 5 ein.
Bei Alpha gibst du 0,05 ein.
Klicke auf ein Feld neben den Daten, um die Output Range festzulegen.
Mit OK schließt du die Analyse ab.
Zweifaktorielle Varianzanalyse in Excel
ANOVA mit Google-Tabellen
Du kannst die beiden Formen der Varianzanalysen gleich selbst mit unserer Google-Tabellen Datei ausprobieren.
Um die einfaktorielle Varianzanalyse zu berechnen, klicke im Menü auf:
- Add-ons
- XLMiner Analysis ToolPak (ist dieses Add-on noch nicht vorhanden, musst du es vorher zu Google-Tabellen hinzufügen)
- Start
- ANOVA: Single Factor
Unter Input Range wählst du die Daten für alle drei Sportarten mitsamt den Labels aus.
Selektiere das Feld Labels in first row.
Bei Output Range wählst du einen Bereich neben den Daten aus. Dort erhältst du die Tabellen mit den Ergebnissen.
Mit OK führst du die Analyse durch.
Einfaktorielle Varianzanalyse in Google-Tabellen
Die zweifaktorielle Varianzanalyse führst du aus mit Klick im Menü auf:
- Add-ons
- XLMiner Analysis ToolPak
- Start
- ANOVA: Two-Factor With Replication (zweifaktorielle Varianzanalyse)
Unter Input Range wählst du alle Daten mitsamt den Labels aus.
Bei Rows per sample gibst du die Zahl 5 ein.
Bei Alpha gibst du 0,05 ein.
Im Feld Output Range wählst du einen Bereich neben den Daten aus, um dir die Ergebnisse dort anzeigen zu lassen.
Mit OK wird die ANOVA berechnet.
Zweifaktorielle Varianzanalyse in Google-Tabellen
ANOVA Ausgabe interpretieren
Nachdem die Analyse durchgeführt wurde, erhältst du von jedem Programm Tabellen mit den Ergebnissen. Diese Ausgabe ist für die einfaktorielle und zweifaktorielle ANOVA unterschiedlich.
Wir erklären dir die Ergebnisse anhand der SPSS-Ausgabe. Die ANOVA Tabellen von Excel und Google-Tabellen sind ähnlich.
Navigiere zwischen den Tabs, um die Interpretation der jeweiligen Ausgabe zu sehen.
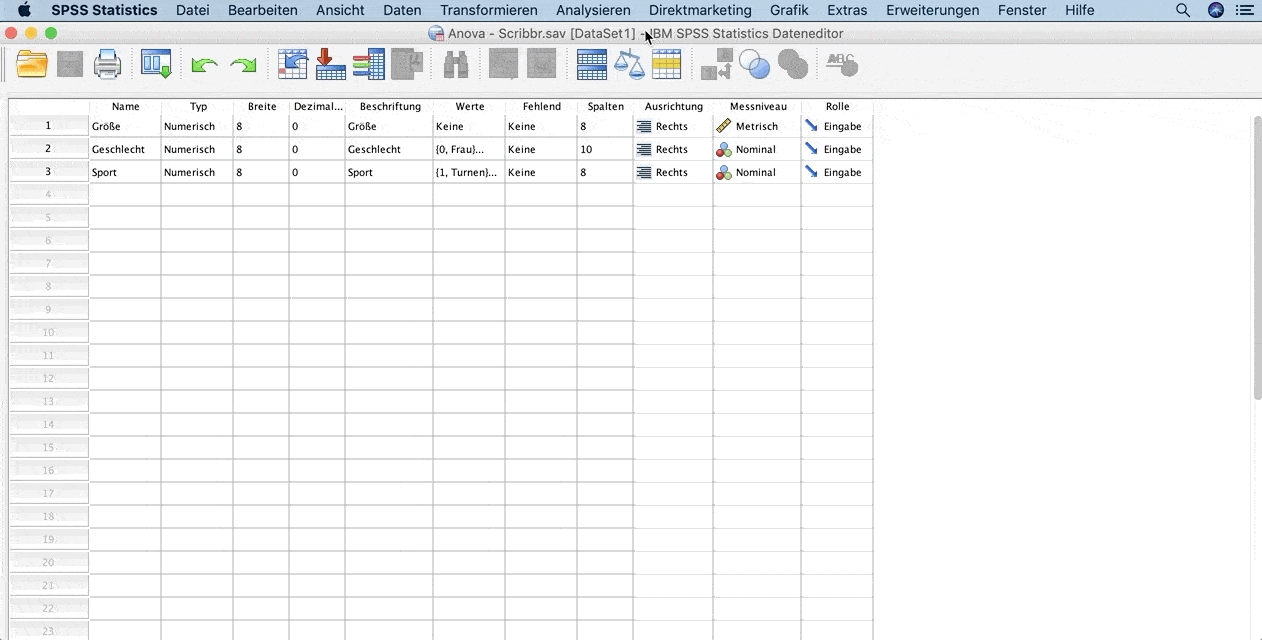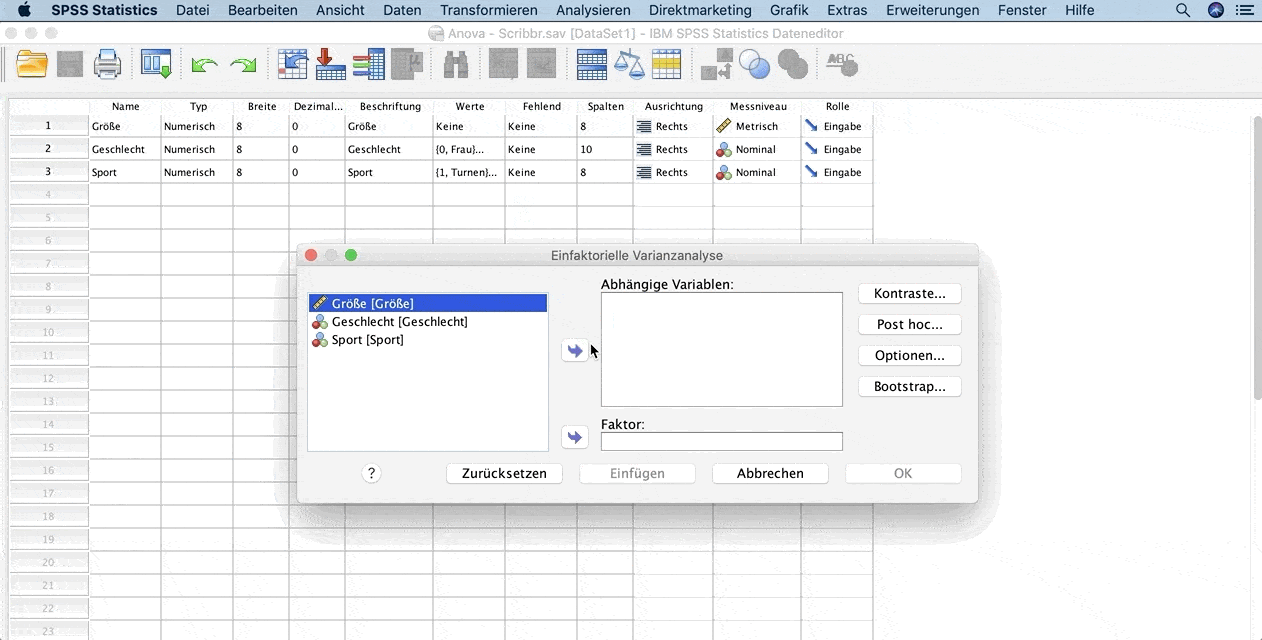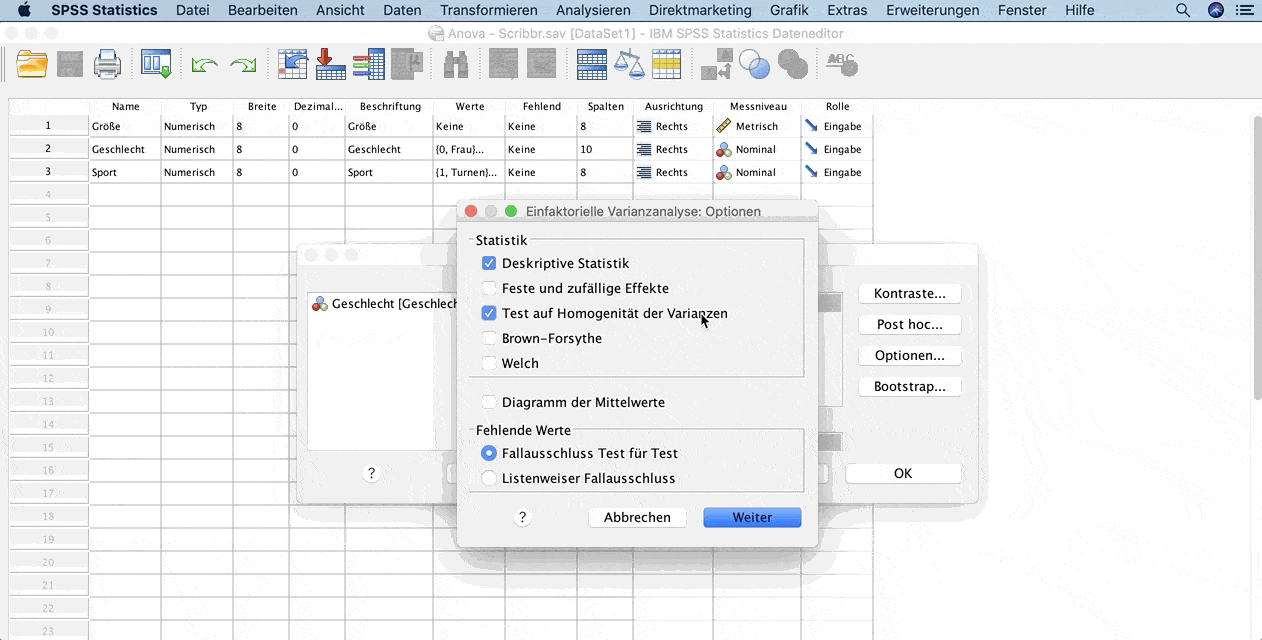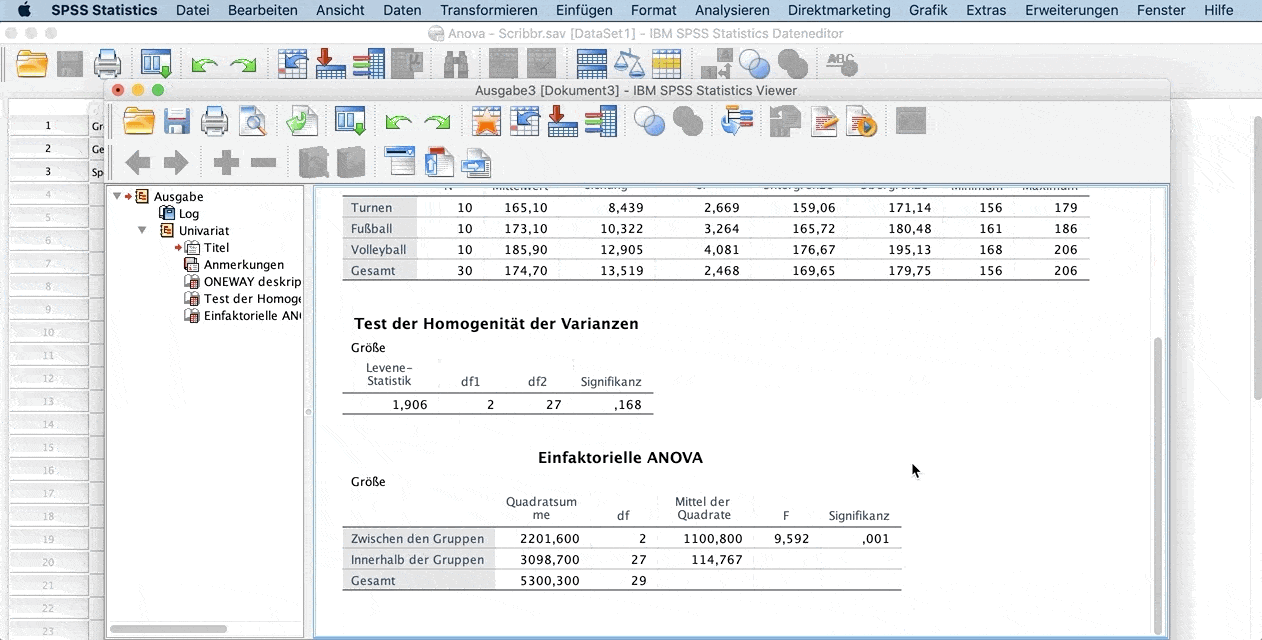
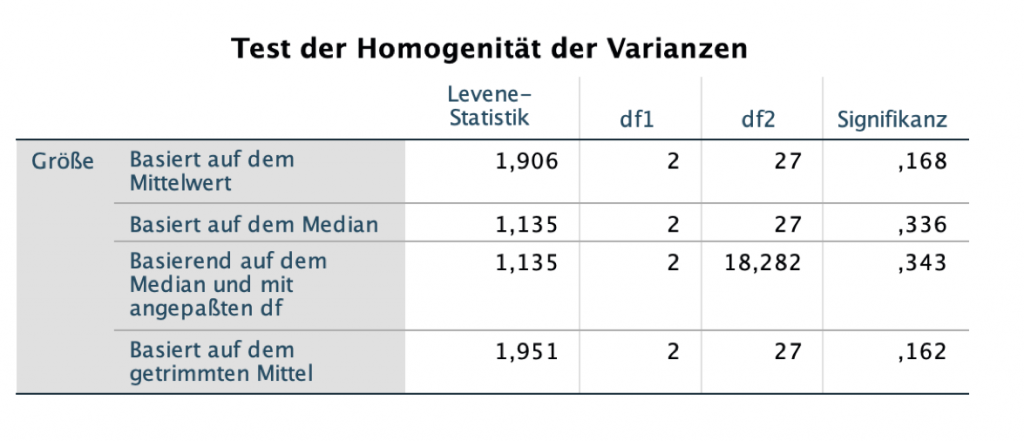
Wenn du dich bei der Analyse entschieden hast zusätzlich auf gleiche Varianzen zu testen, erhältst du zwei relevante Tabellen:
- Test der Homogenität der Varianzen und
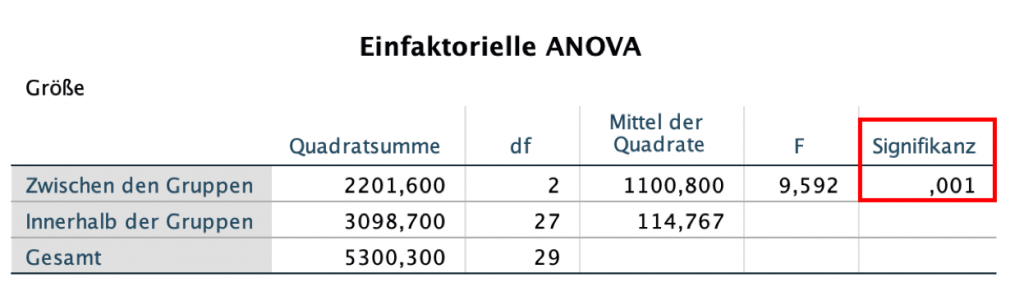
- Einfaktorielle ANOVA
Der Test zur Homogenität der Varianzen erlaubt den Schluss, dass die Bedingung gleicher Varianzen für die verschiedenen Gruppen zutrifft.
Dafür schaust du dir die Signifikanz der Zeile Größe – Basiert auf dem Mittelwert an. Wenn dieser Wert größer als 0.050 ist, dann sind die Varianzen gleich (hier: 0.168).
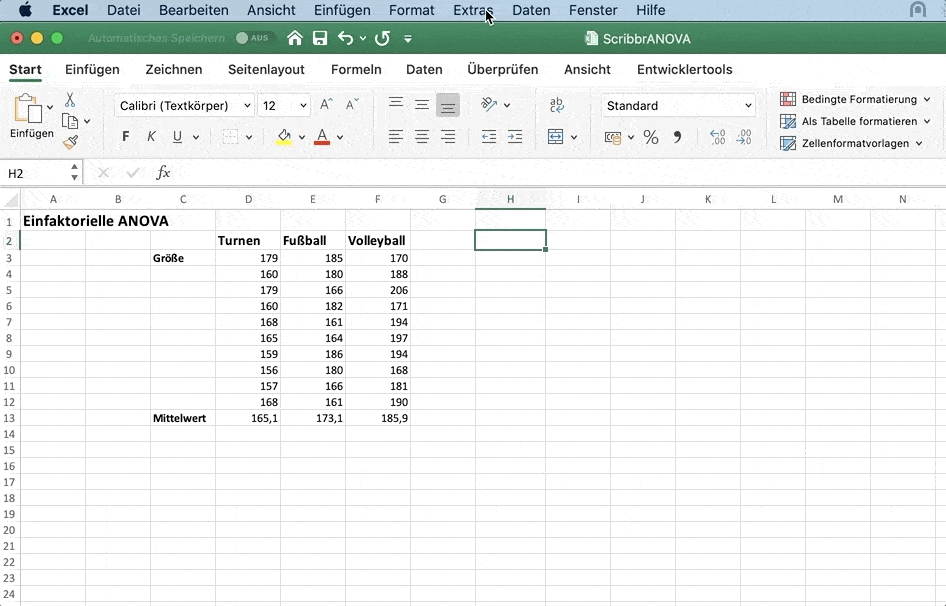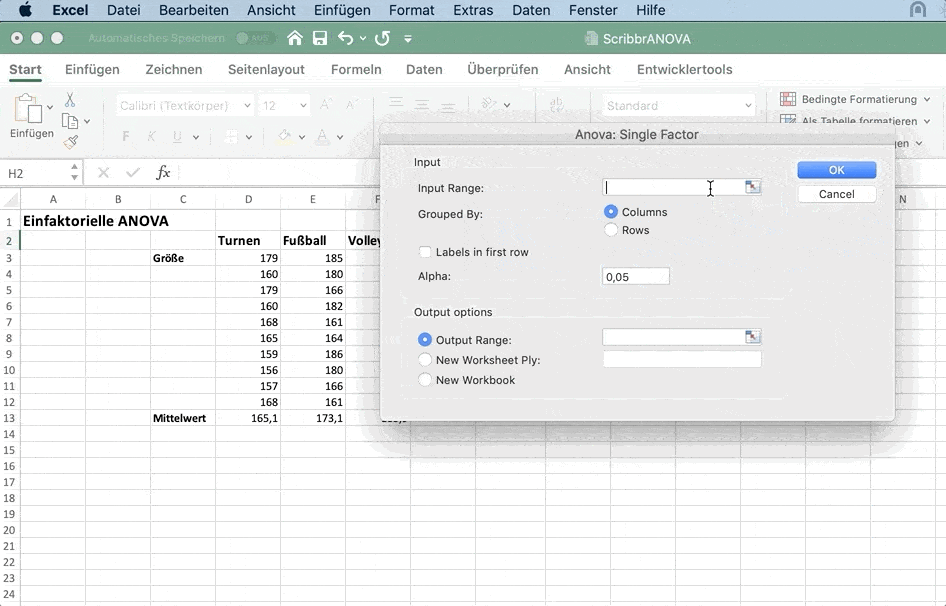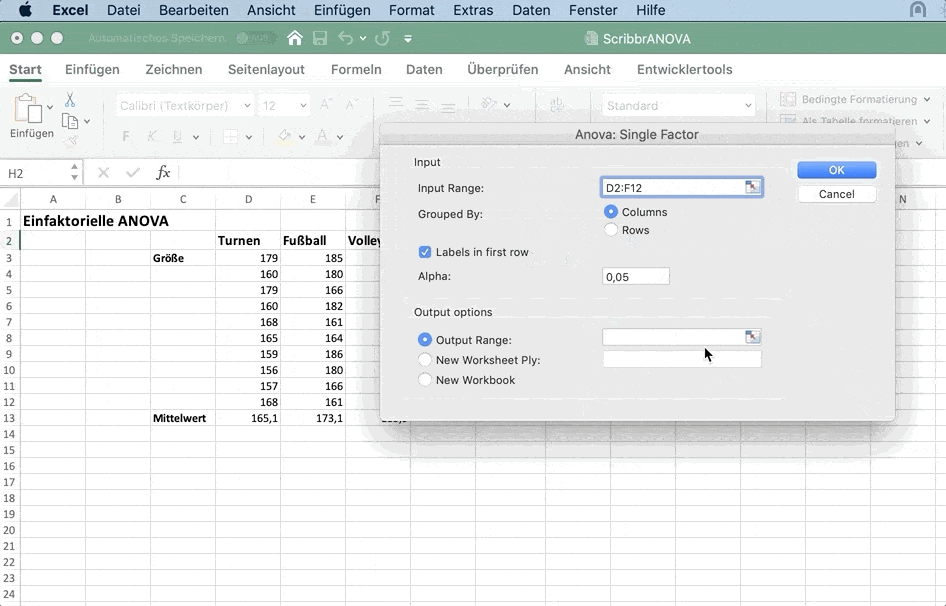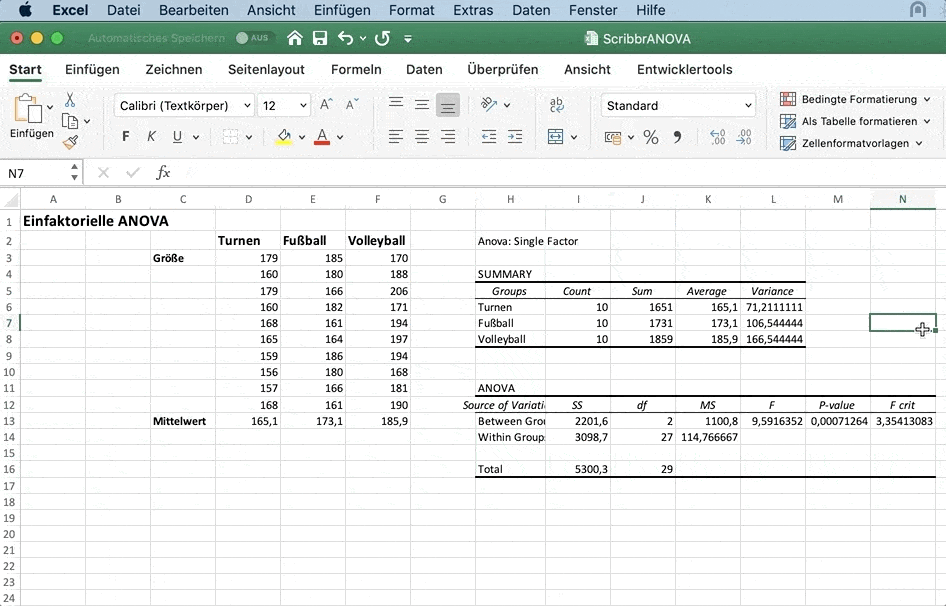
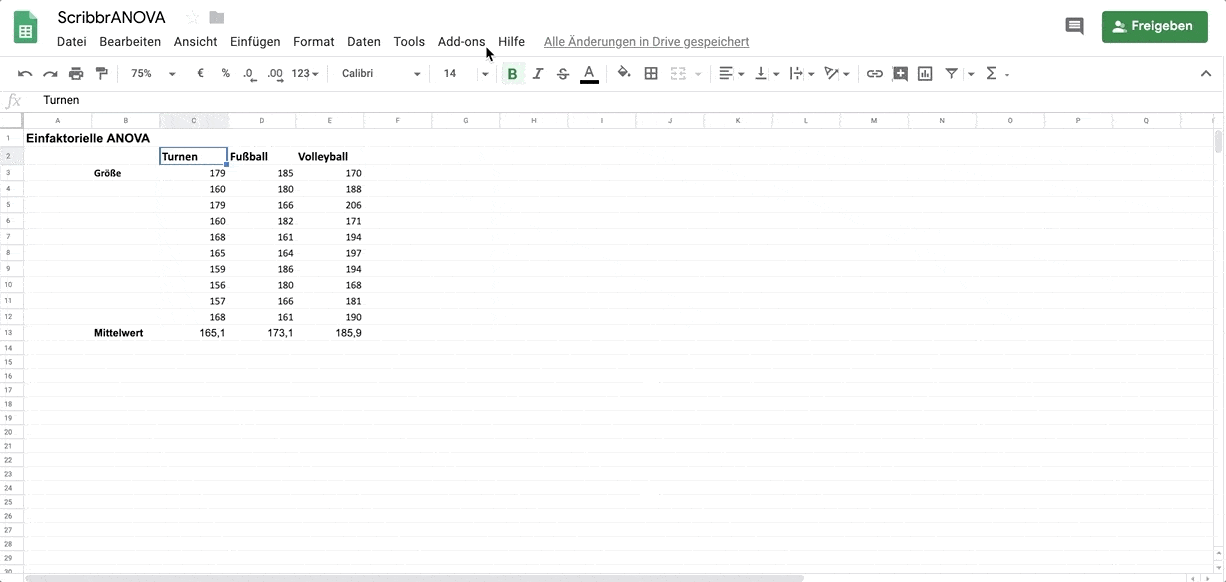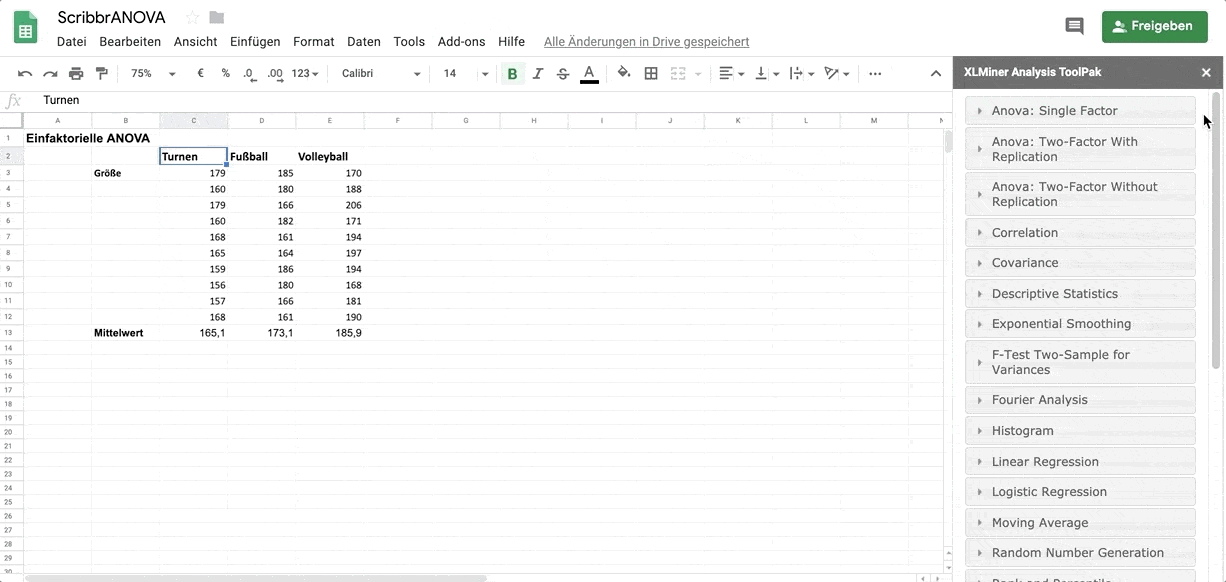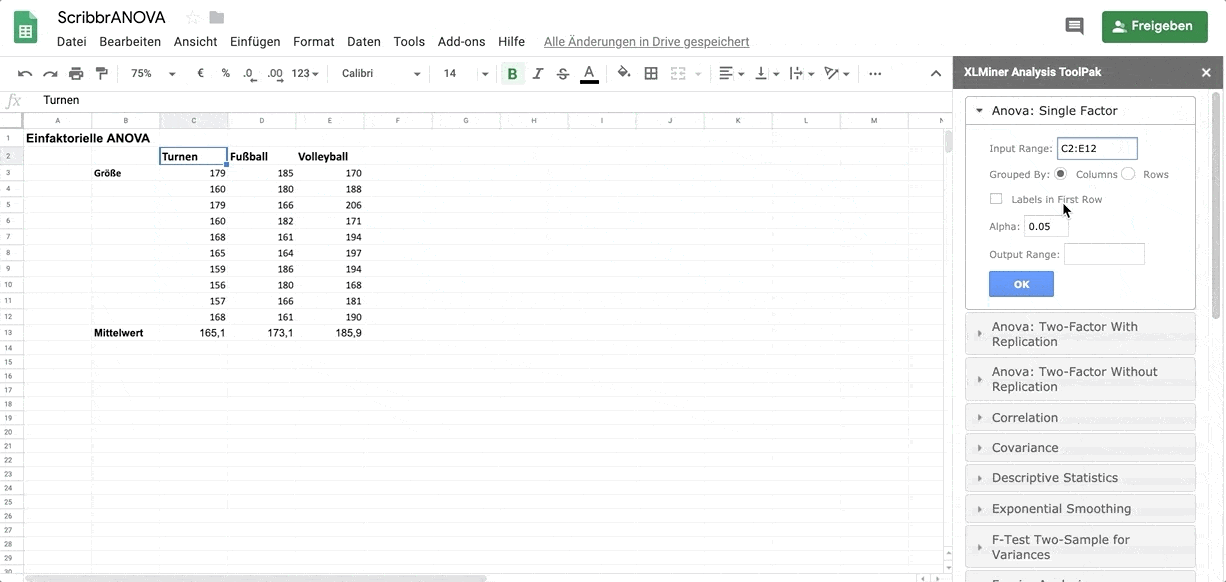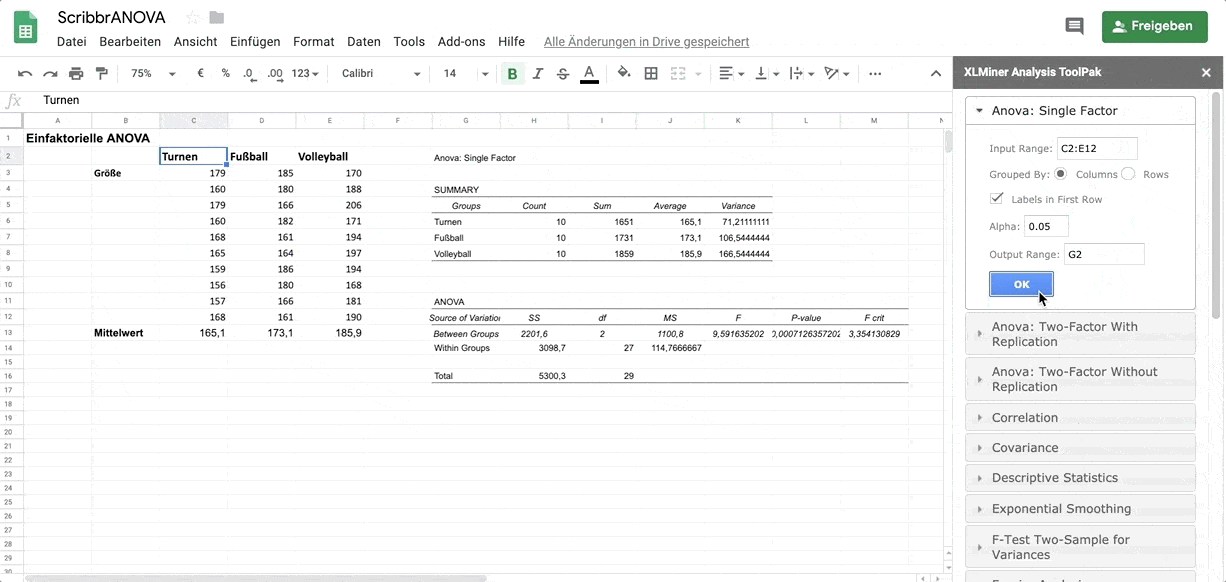
Die zweite Tabelle zeigt das Ergebnis der einfaktoriellen ANOVA.
Hier wird getestet, ob ein signifikanter Teil der Varianz durch die Gruppenvariable erklärt wird. Dafür wird ein F-Test mit 2 Freiheitsgraden (die Anzahl der Gruppen = 3 minus 1) und 27 (die Anzahl der Beobachtungen = 30 minus der Anzahl der Gruppen (3)) durchgeführt.
Die Wahrscheinlichkeit, einen F-Wert von 9.592 oder größer mit diesen Freiheitsgraden zu erhalten, liegt bei 0.001, wie sich der Spalte Signifikanz entnehmen lässt.
Wir können daher schließen, dass sich die Gruppenmittelwerte voneinander unterscheiden.
Die Mittel der Quadrate zeigen, wie viel der Varianz zwischen den Gruppen und innerhalb der Gruppen liegt. Je mehr Varianz es zwischen den Gruppen gibt, umso besser sagen die Gruppen die Größe vorher.
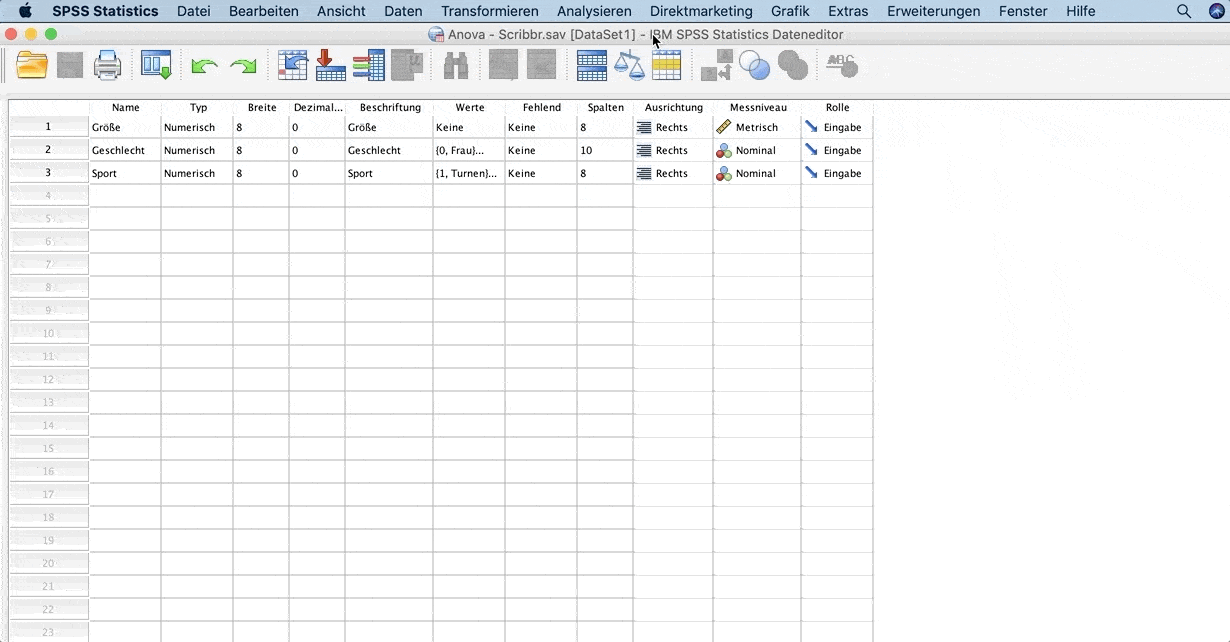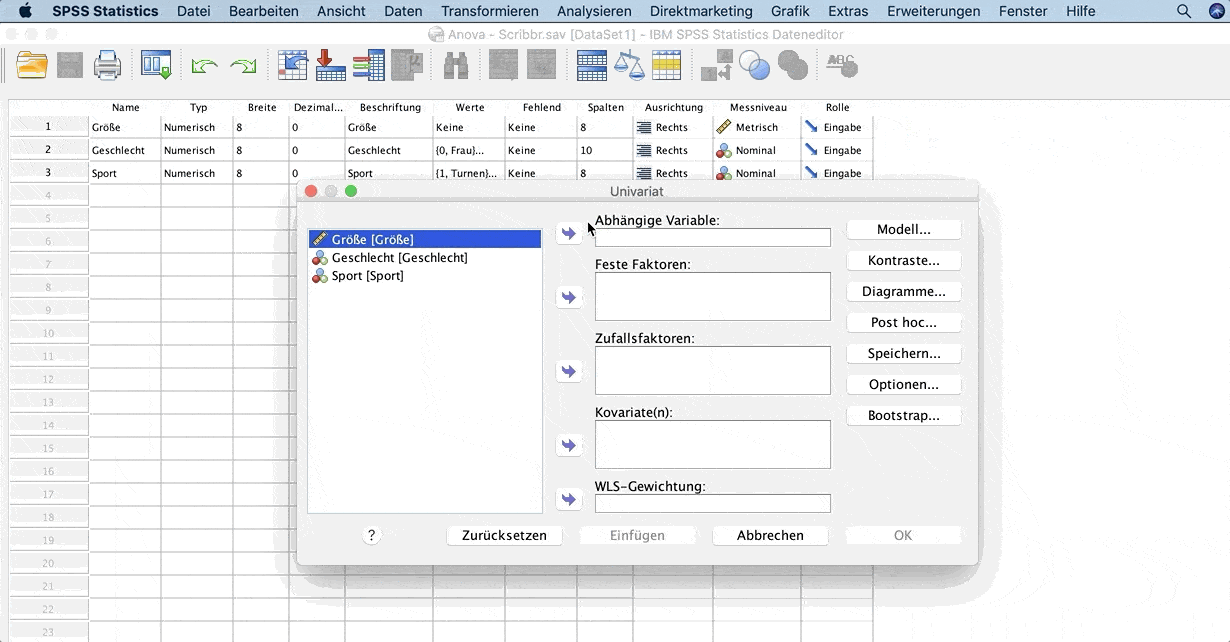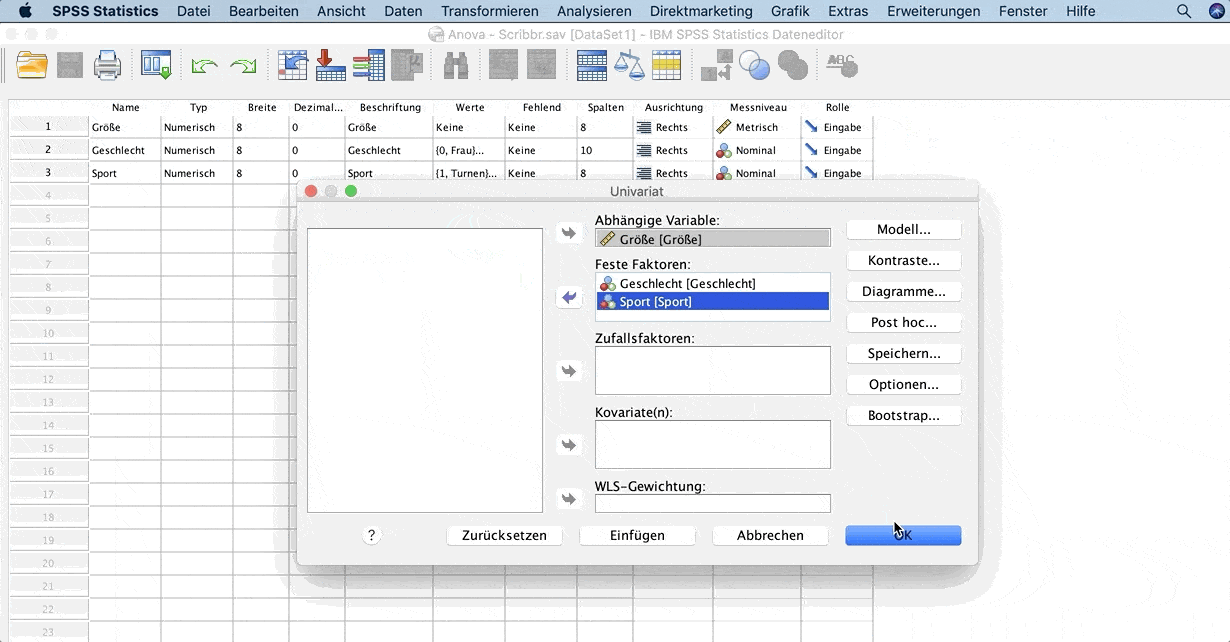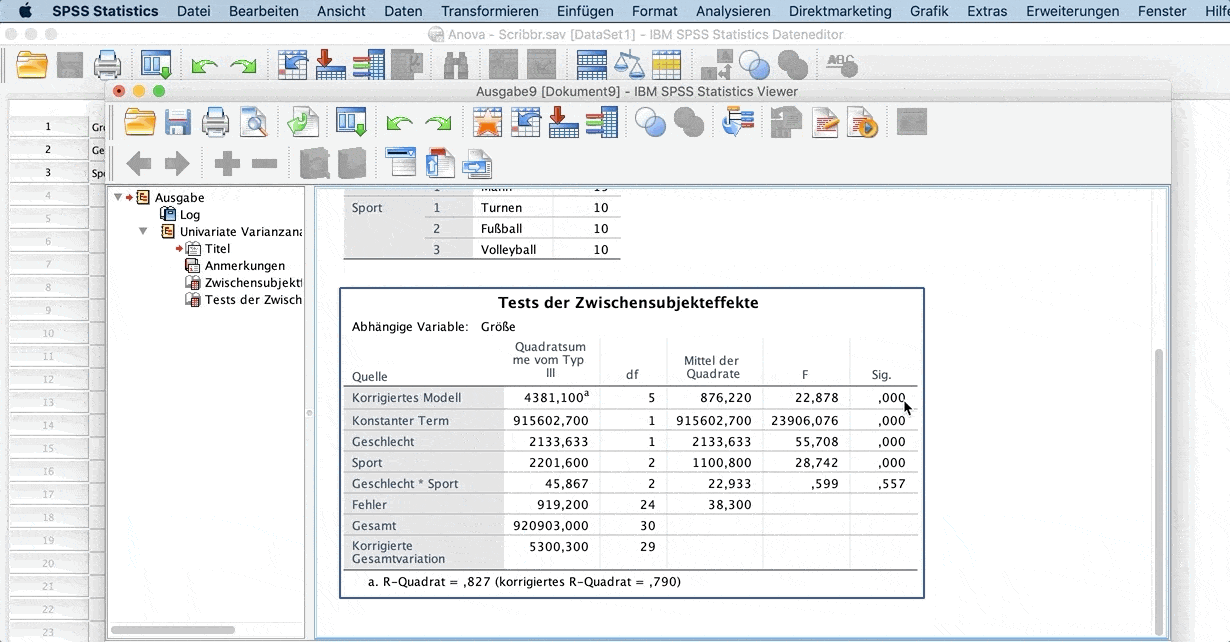
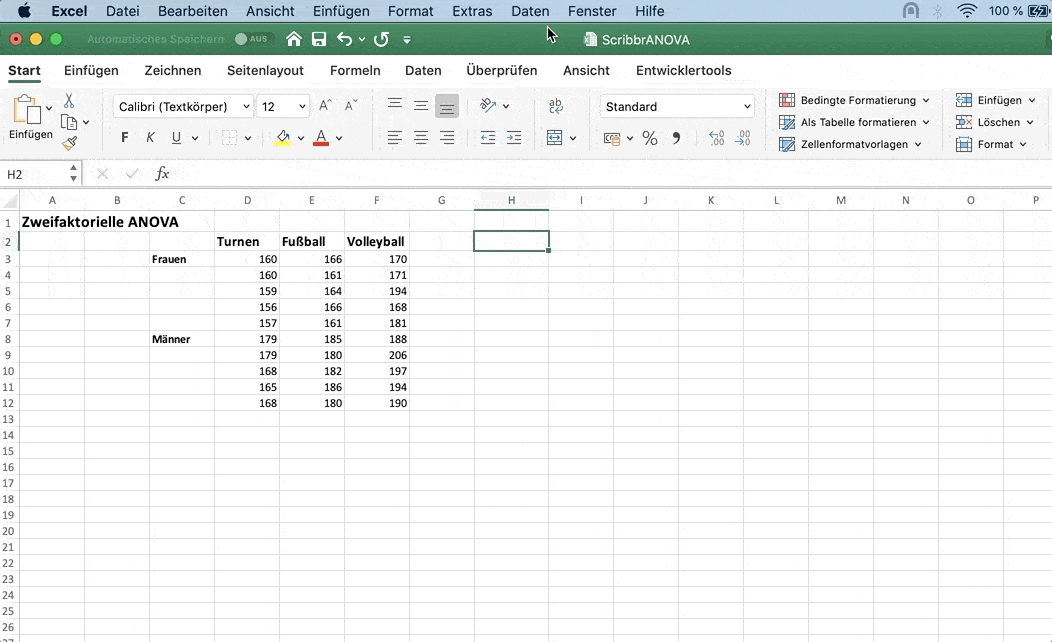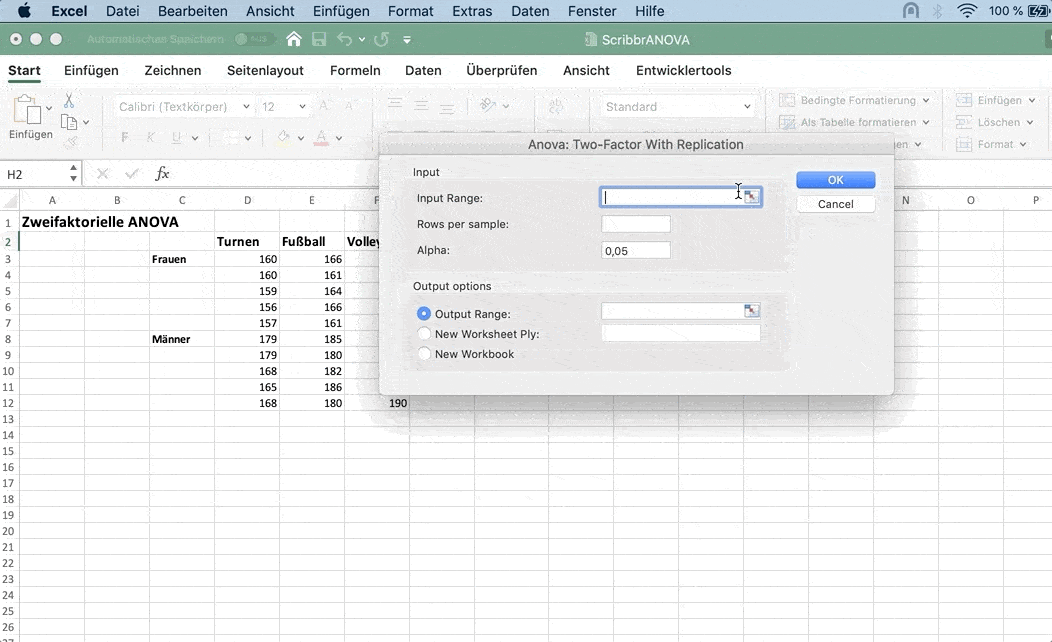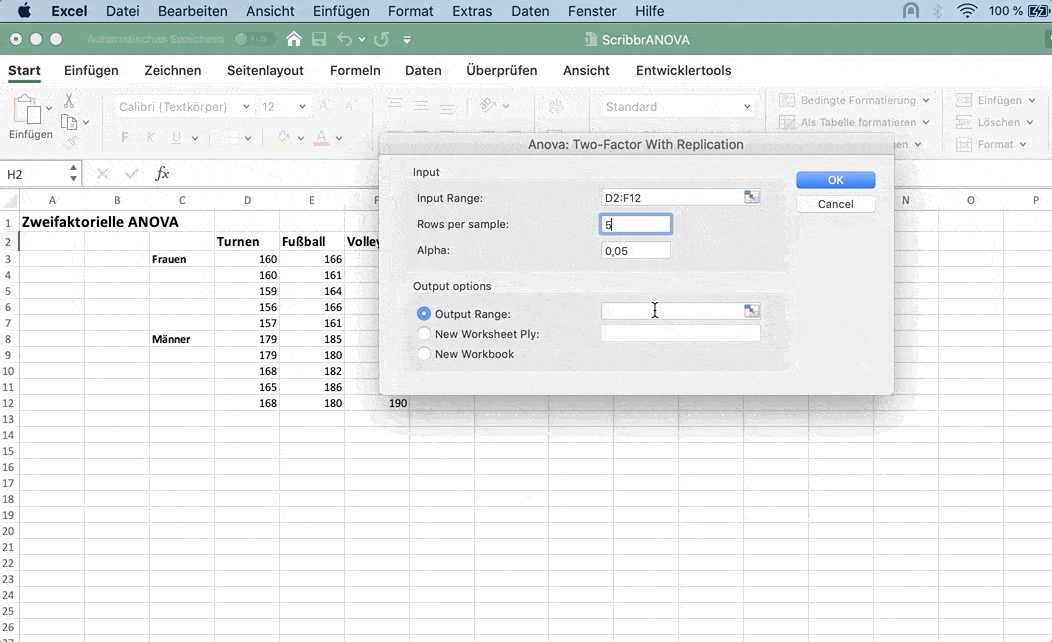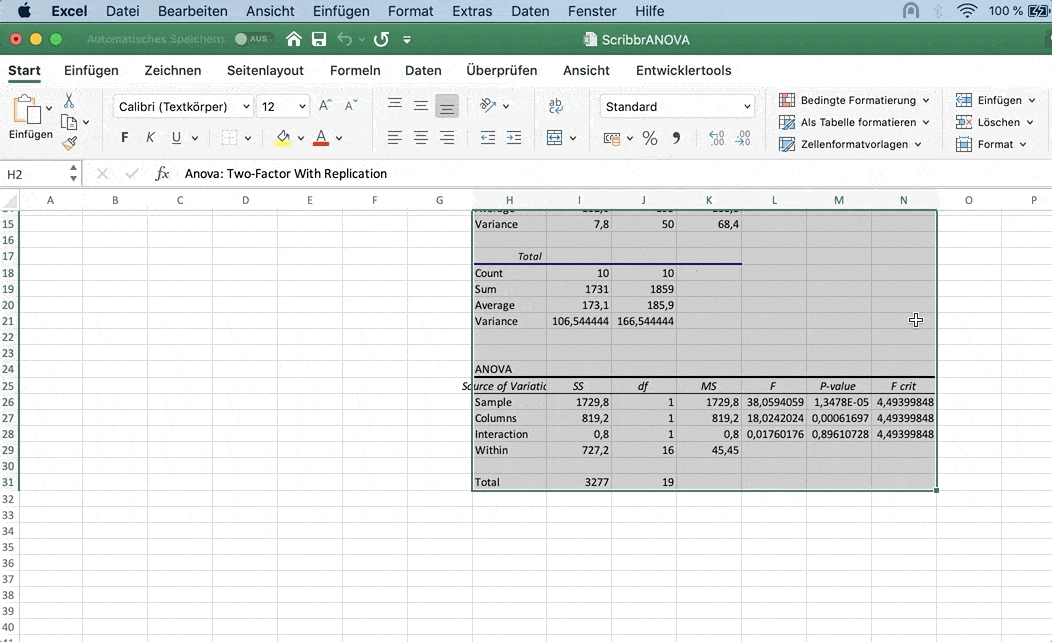
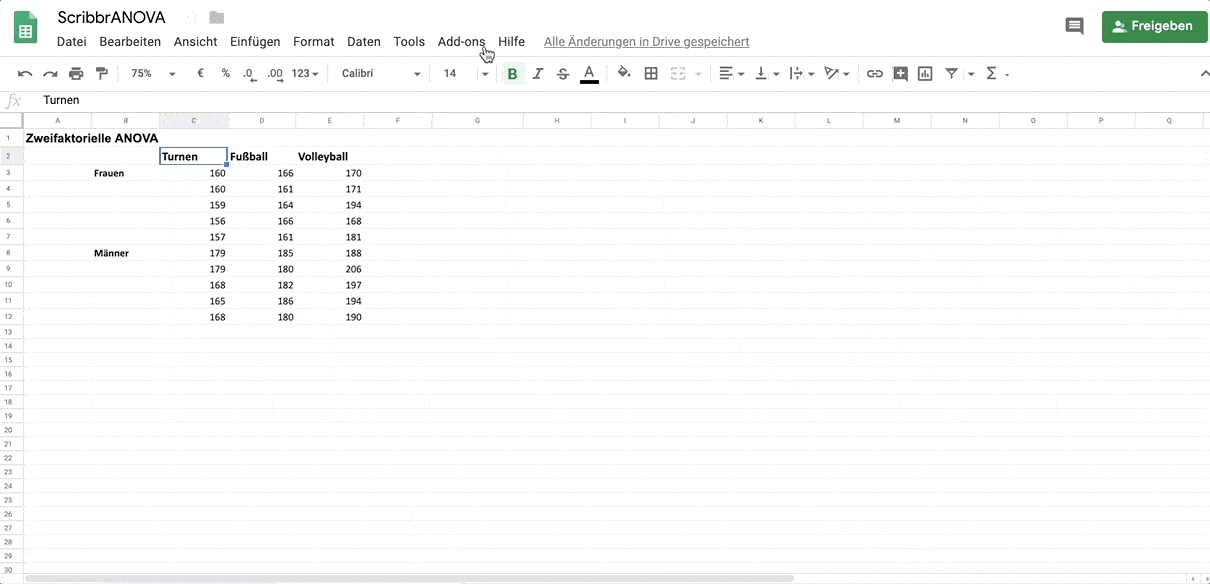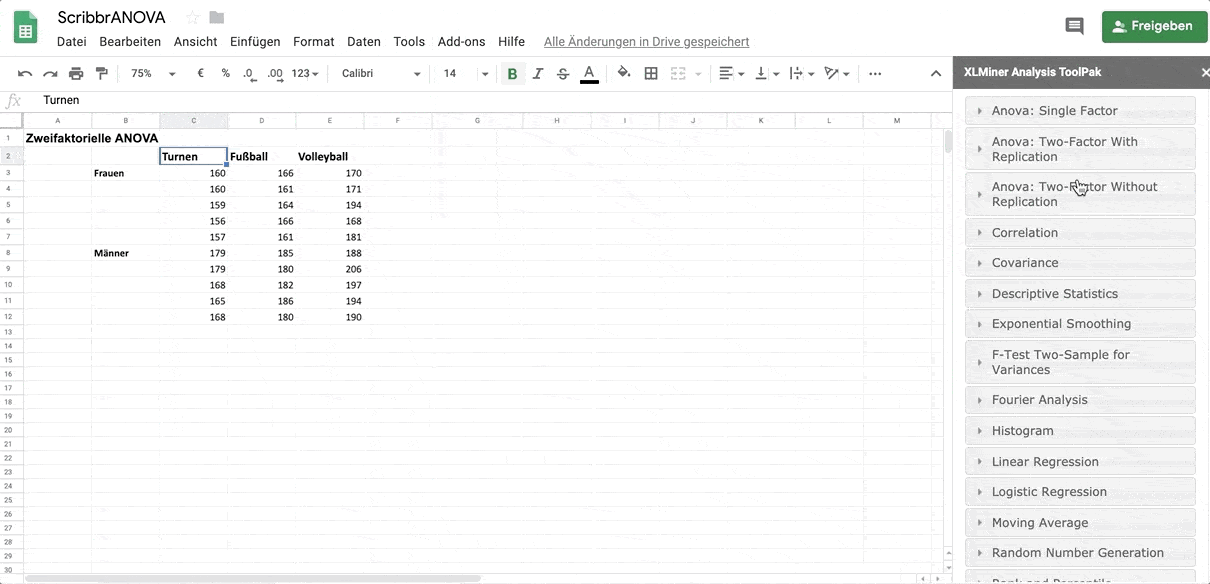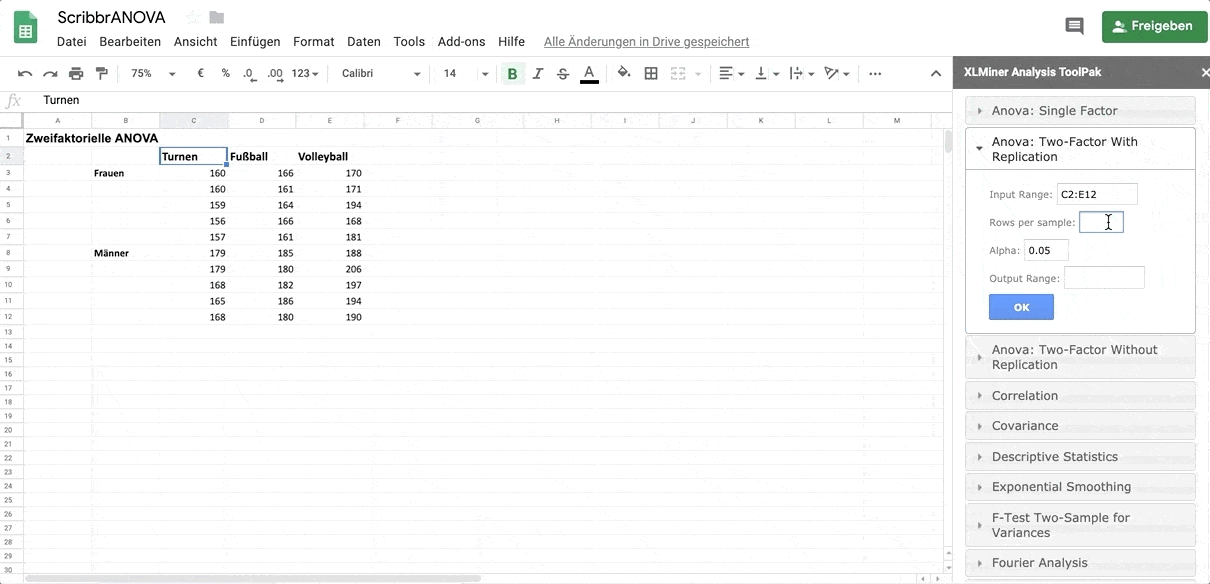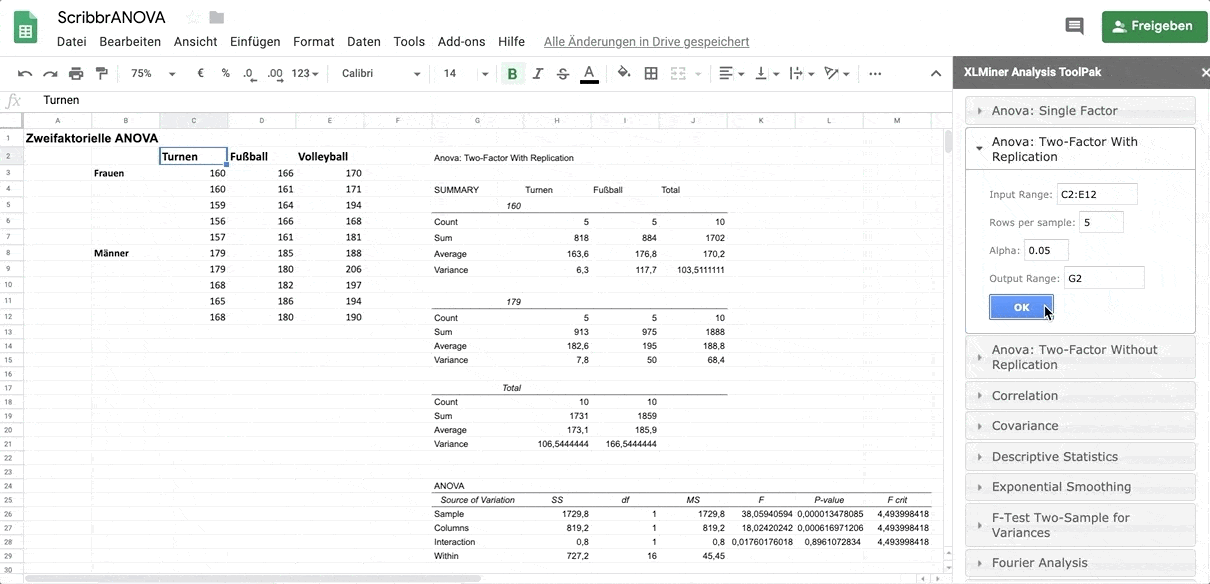
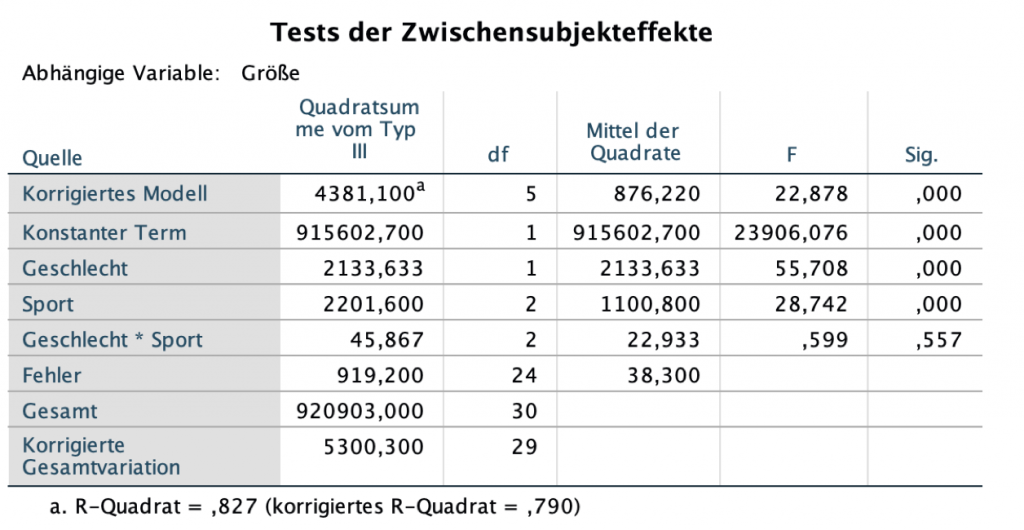
Die Ausgabe der zweifaktoriellen ANOVA besteht aus einer Anzahl von Tabellen mit deskriptiven Statistiken wie z. B. den Mittelwerten für jede Gruppe. Die wichtigste Tabelle ist Tests der Zwischensubjekteffekte.
Hier wird getestet, ob ein signifikanter Teil der Varianz durch die Gruppenvariablen erklärt wird. Dafür wird ein F-Test mit 5 Freiheitsgraden (Anzahl der Gruppen von Athleten = 3 mal der Anzahl der Geschlechter = 2 minus 1) und 24 (Zahl der Beobachtungen = 30 minus der Anzahl der Gruppen der Athleten = 3 mal der Anzahl der Geschlechter (2)) durchgeführt.
Die Wahrscheinlichkeit einen F-Wert von 22.878 oder größer mit diesen Freiheitsgraden zu erhalten ist geringer als 0.001, wie sich der Spalte Sig. entnehmen kann.
Wir können also schließen, dass sich die Mittelwerte der Gruppen unterscheiden.
Das bedeutet, dass der Unterschied zwischen den Athleten in Bezug auf die Größe nicht durch ihr Geschlecht beeinflusst wird.
Post-hoc Tests
Du weißt nun, dass sich einige Gruppen der Athleten und Athletinnen signifikant voneinander unterscheiden.
Um herauszufinden, welche Gruppen sich signifikant unterscheiden, kannst du Post-hoc-Tests durchführen.
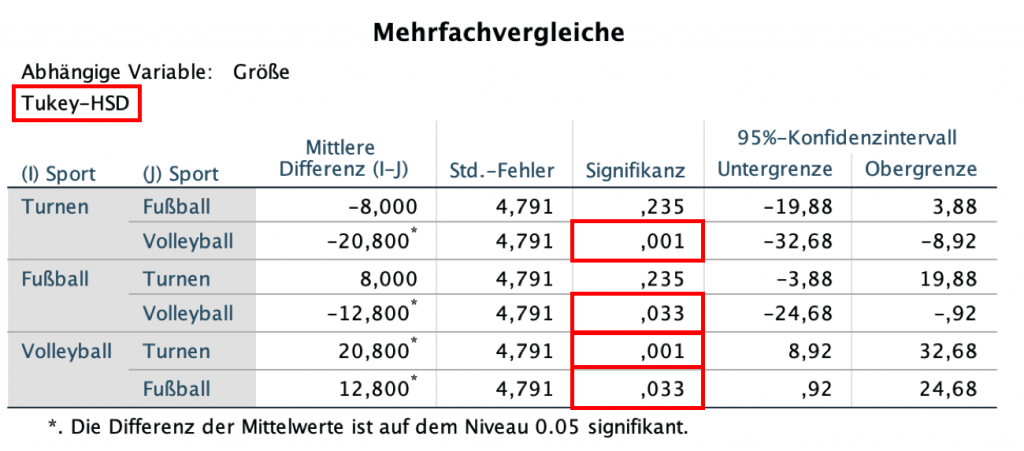
Du führst die ANOVA mit SPSS noch einmal durch und klickst auf Post-hoc.
Du musst dann Tests für gleiche und ungleiche Varianzen auswählen. Wenn die Varianzen gleich sind, wird Tukey oft verwendet. Wird nicht davon ausgegangen, dass die Varianzen gleich sind, wird häufig Games-Howell ausgewählt.
In unserem Datensatz sind die Varianzen bei der einfaktoriellen ANOVA gleich (jedoch nicht bei der zweifaktoriellen ANOVA). Also verwenden wir Tukey.
Eine weitere Tabelle mit dem Namen Mehrfachvergleiche wurde der SPSS-Ausgabe hinzugefügt.
In der Spalte Signifikanz siehst du dir die Unterschiede an, die signifikant sind (p < 0.050).
Ergebnisse der ANOVA zusammenfassen
Du fasst die Ergebnisse deiner ANOVA im Ergebniskapitel deiner Bachelorarbeit oder Masterarbeit zusammen. Du gibst den F-Wert mit seinen Freiheitsgraden und der Signifikanz an. Falls du einen Post-hoc-Test durchgeführt hast, beschreibst du dessen Ergebnisse ebenfalls.
- Es gibt einen signifikanten Unterschied im Zusammenhang der durchschnittlichen Größe zwischen den drei Gruppen der Athleten (F (2.27) = 9.952; p = 0.001). Es gibt keinen signifikanten Unterschied im Zusammenhang der Größe zwischen Turnern und Fußballspielern (p = 0.235).
- Eine ANOVA zeigt, dass ein signifikanter Unterschied im Zusammenhang der Größe zwischen Personen besteht, die unterschiedliche Sportarten ausüben, F (2.27) = 9.952; p = 0.001. Volleyballspieler sind signifikant größer als Fußballspieler (p = 0.033) und Turner (p = 0.001). Ein signifikanter Unterschied zwischen der Größe von Turnern und Fußballspielern wurde hingegen nicht gefunden (p = 0.235).
Statistische Bedingungen für ANOVA
Bevor du eine ANOVA durchführen kannst, müssen deine Daten bestimmte statistische Bedingungen erfüllen. Wenn das nicht der Fall ist, wirst du vermutlich falsche Schlüsse aus den Ergebnissen ziehen.
Die Bedingungen für Varianzanalysen sind:
- Die abhängige Variable ist ratio- oder intervallskaliert.
- Die Daten pro Gruppe stammen aus einer Zufallsstichprobe.
- Die Varianzen für jede Gruppe sind gleich (Homoskedastizität). Das kann mit dem Homogenitätstest der Varianzen überprüft werden.
- Die Daten innerhalb jeder Gruppe sind normalverteilt.
Formel F-Wert
Auch wenn Programme wie SPSS, Excel oder Google-Tabellen die ANOVA für dich berechnen, ist es manchmal nützlich, wenn du die Formel kennst.
Angenommen, es gibt k Gruppen mit der Gruppengröße g, dann wird der F-Wert der einfaktoriellen ANOVA so berechnet:
x̄j = Mittelwert der Gruppe j
Die Anzahl der Freiheitsgrade des F-Wertes ist gleich den Divisoren des Zählers und des Nenners, also (k – 1) und (N – k).
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Flandorfer, P. (2023, 30. Januar). ANOVA - Varianzanalyse durchführen und interpretieren. Scribbr. Abgerufen am 16. Dezember 2024, von https://www.scribbr.de/statistik/anova-varianzanalyse/
