Die Lageparameter erklärt mit Beispielen
Lageparameter werden in der deskriptiven Statistik verwendet, um die zentrale Lage einer Verteilung von Daten anzugeben, also zum Beispiel den Mittelwert oder den Zentralwert.
Lageparameter ist der Überbegriff für die Werte, die wir als arithmetisches Mittel, den Median oder den Modus bestimmen.
Eine andere Bezeichnung für Lageparameter ist auch Lagemaß.
Lageparameter im Überblick
Die Tabelle gibt dir einen Überblick über die wichtigsten Lageparameter – das arithmetische Mittel, den Median und den Modus.
| Überblick der Lageparameter | |
|---|---|
| Arithmetisches Mittel (auch: Mittelwert oder Durchschnittswert) |
statistischer Durchschnittswert Zur Berechnung addieren wir alle Beobachtungsdaten und teilen dann die Summe durch die Anzahl der Daten. |
| Beispiel Die Körpergröße von acht Personen (in cm): 150, 155, 160, 165, 170, 175, 180, 185 Arithmetisches Mittel: 167.5 |
|
| Median | Wert, der genau in der Mitte einer Datenreihe liegt, die nach der Größe geordnet ist |
| Beispiel geordnete Datenreihe: 10, 20, 30, 40, 50, 60, 70 Median: 40 |
|
| Modus | Wert, der in einem Datensatz am häufigsten vorkommt |
| Beispiel Beobachtungsdaten: 30, 25, 21, 26, 21, 25, 23, 26, 29, 18, 30, 25 Modus: 25 |
|
Verwendung der Lageparameter
Wann wir das arithmetische Mittel, den Median oder den Modus anwenden können, hängt von den Eigenschaften unserer Daten ab. Diese Eigenschaften werden auch als Skalenniveau bezeichnet und können nominal, ordinal oder metrisch sein.
Die Tabs geben dir einen Überblick über die Skalenniveaus und wann du welchen Lageparameter bestimmen kannst.
| Erklärung | mögliche Lageparameter |
|---|---|
| Nominale Daten können wir nicht in eine Rangreihenfolge bringen. Dies bedeutet, dass wir nicht sagen können, dass ein Wert besser oder schlechter als ein anderer ist, sondern nur, ob es einen Unterschied gibt.
Beispiel: Haarfarbe, Geschlecht, Geburtsort oder Postleitzahl |
Modus |
| Erklärung | mögliche Lageparameter | |
|---|---|---|
| Ordinalskalierte Daten können wir in eine Reihenfolge bringen, aber wir können keine Aussage über die Abstände machen, das heißt, wir können z.B. nicht sagen, dass die Note 2 halb so gut ist wie die Note 4.
Beispiel: Schulnoten, Zufriedenheit (z.B auf einer Skala von 1-5) |
Modus | |
| Erklärung | mögliche Lageparameter | |
|---|---|---|
| Bei Metrischen Daten können wir eine Rangreihenfolge erstellen und auch Aussagen über die Abstände treffen, wie z. B., dass jemand mit einem Alter von 50 doppelt so alt ist wie eine 25-jährige Person.
Beispiel: Temperatur, Einkommen, Alter, Körpergröße |
Modus Median arithmetisches Mittel |
|
Lageparameter am Beispiel erklärt
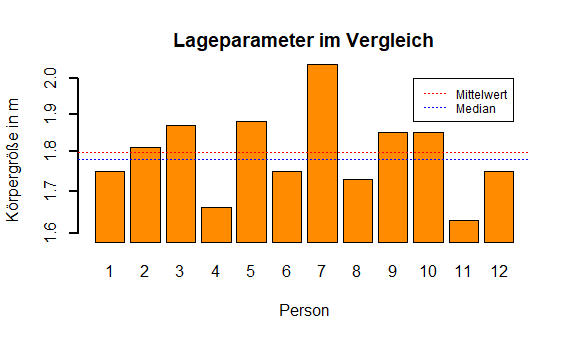
Nehmen wir an, wir haben 12 Menschen nach ihrer Körpergröße gefragt und folgende Antworten erhalten:
| Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Körpergröße in m | 1.75 | 1.82 | 1.87 | 1.66 | 1.88 | 1.75 | 2.04 | 1.73 | 1.85 | 1.85 | 1.63 | 1.75 |
Die Abbildung zeigt die verschiedenen Körpergrößen der Personen. Wir sehen, dass die Werte für den Mittelwert (rote Linie) und den Median (blaue Linie) unterschiedlich sind.
| Erklärung |
|---|
| Beim Median bestimmen wir, welcher Wert genau in der Mitte der geordneten Reihe aller Beobachtungsdaten liegt und diese in zwei Hälften teilt. |
| Berechnung |
geordnete Reihe: 1.63, 1.66, 1.73, 1.75, 1.75, 1.75, 1.81, 1.85, 1.85, 1.87, 1.88, 2.04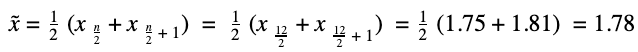 |
| Ergebnis |
| Der Median ist 1.78 m.
Eine Körpergröße von 1.78 m liegt genau in der Mitte der geordneten Datenreihe und teilt die Gruppe in zwei Hälften. Dabei ist die eine Hälfte der Gruppe (mit den Körpergrößen 1.63, 1.66, 1.73, 1.75, 1.75, 1.75) kleiner als der Median 1.78 m und die andere Hälfte (mit den Körpergrößen 1.81, 1.85, 1.85, 1.87, 1.88, 2.04) größer als der Median 1.78 m. |
| Erklärung |
|---|
| Beim arithmetischen Mittel bestimmen wir den durchschnittlichen Wert aller Beobachtungsdaten. |
| Berechnung |
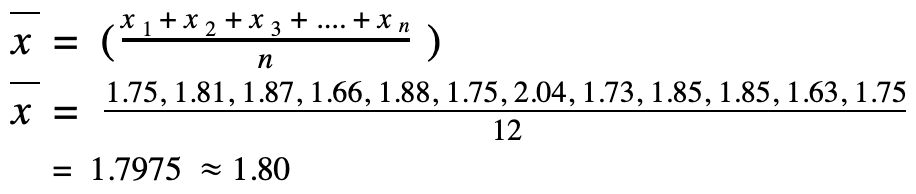 |
| Ergebnis |
| Das arithmetische Mittel der Körpergröße der Gruppe beträgt 1.80 m. Im Durchschnitt sind die Personen in der Gruppe also 1.80 m groß. |
| Erklärung | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beim Modus bestimmen wir, welcher Wert in unseren Beobachtungsdaten am häufigsten vorkommt. | ||||||||||||||||||||
| Berechnung | ||||||||||||||||||||
|
||||||||||||||||||||
| Ergebnis | ||||||||||||||||||||
| Der Modus beträgt 1.75 m. Diese Körpergröße kommt am häufigsten in der Gruppe vor. |
Häufig gestellte Fragen
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2023, 23. Mai). Die Lageparameter erklärt mit Beispielen. Scribbr. Abgerufen am 2. Juli 2025, von https://www.scribbr.de/statistik/lageparameter/