Den T-Test verstehen und interpretieren mit Beispiel
Den t-Test, auch als Student’s t-Test bezeichnet, verwendest du, wenn du die Mittelwerte von maximal zwei Gruppen miteinander vergleichen möchtest.
Zum Beispiel kannst du mit dem t-Test analysieren, ob Männer im Durchschnitt größer als Frauen sind.
Wenn du hingegen die Mittelwerte von mehr als zwei Gruppen vergleichen willst, kannst du eine ANOVA oder eine multiple Regression mit Dummy-Variablen wählen.
Formen des t-Tests
Diese Formen des t-Tests gibt es:
- Einstichproben–t-Test,
- Zweistichproben-t-Test und
- abhängiger t-Test.
Welchen t-Test du wählen solltest, hängt von den Mittelwerten ab, die du vergleichen möchtest.
Einstichproben-t-Test
Verwende den Einstichproben-t-Test, wenn du untersuchen möchtest, ob sich der Mittelwert einer Stichprobe von einem bestimmten Wert unterscheidet.
Zweistichproben-t-Test
Wenn du testen möchtest, ob sich die Mittelwerte zweier Stichproben voneinander unterscheiden, verwendest du den Zweistichproben-t-Test.
Abhängiger t-Test
Der abhängige t-Test wird verwendet, wenn zwei Mittelwerte von miteinander verbundenen (abhängigen) Stichproben verglichen werden sollen.
Für unser Beispiel verwenden wir den Zweistichproben-t-Test. Er wird von allen Varianten des t-Tests am häufigsten genutzt. Die Auswertungsschritte und die SPSS-Ausgabe für den Einstichproben- und den Zweistichproben-t-Test sind ähnlich.
Um den Zweistichproben-t-Test mit SPSS durchzuführen, klick im Menü auf Folgendes:
- Analysieren
- Mittelwerte vergleichen
- t-Test bei unabhängigen Stichproben (oder t-Test bei einer Stichprobe oder t-Test bei verbundenen Stichproben)
Ein Fenster öffnet sich. Wähl dann
- unter Testvariable(n) die Variable Größe und
- unter Gruppierungsvariable die Variable Geschlecht aus.
- Klick auf Gruppen definieren und gib bei Gruppe 1 und Gruppe 2 die Werte ein, die du verwendest, z. B. Frauen = 0, Männer = 1.
- Du kannst die relevanten Werte der Variable Geschlecht in der Variablenansicht nachsehen.
Klick auf Ok, um den t-Test durchzuführen.
Verwende unsere Excel-Datei, um mit diesen Daten zu üben. Geh dafür im Menü auf diese Auswahloptionen:
- Extras
- Datenanalyse
- t-Test: Two-Sample Assuming Equal Variances
Variable 1 Range: Hier wählst du alle Daten zur Größe der Frauen aus (inklusive des Labels).
Variable 2 Range: Hier wählst du alle Daten zur Größe der Männer aus (inklusive des Labels).
Selektier Labels
Unter Output Options wähl New Worksheet Ply und gib t-Test ein.
Klick auf Ok.
Du kannst den t-Test mit unserer Google-Tabellen-Datei selbst üben. Um statistische Analysen mit Google-Tabellen durchführen zu können, musst du das Add-On XLMiner Analysis ToolPak hinzufügen. Um den t-Test mit Google-Tabellen zu berechnen, klick im Menü auf diese Auswahloptionen:
- Add-Ons
- XLMiner Analysis ToolPak: Start
- t-Test: Two-Sample Assuming Equal Variances
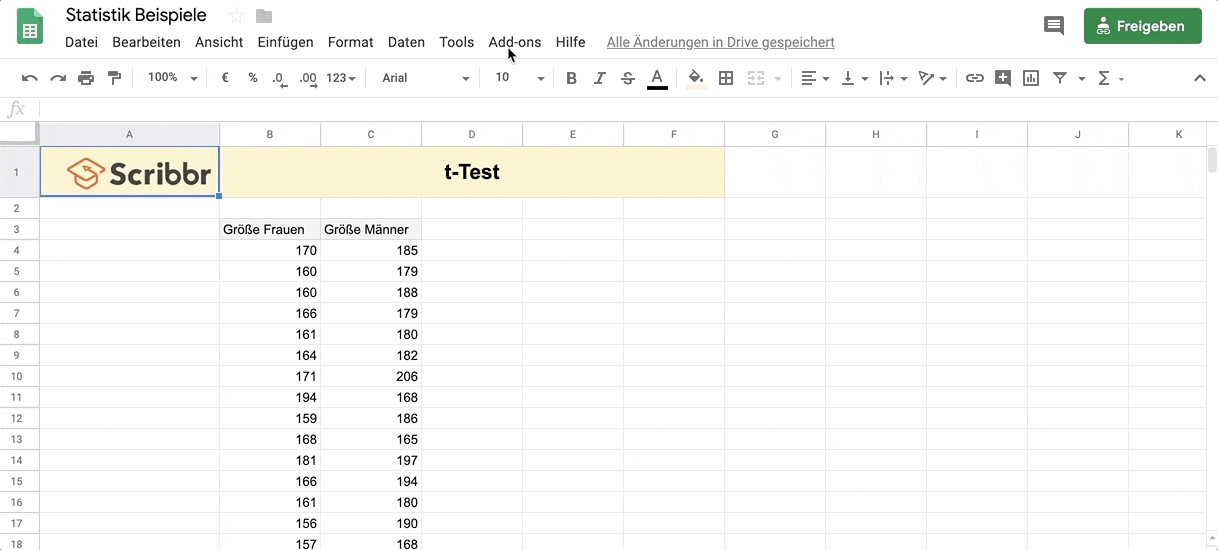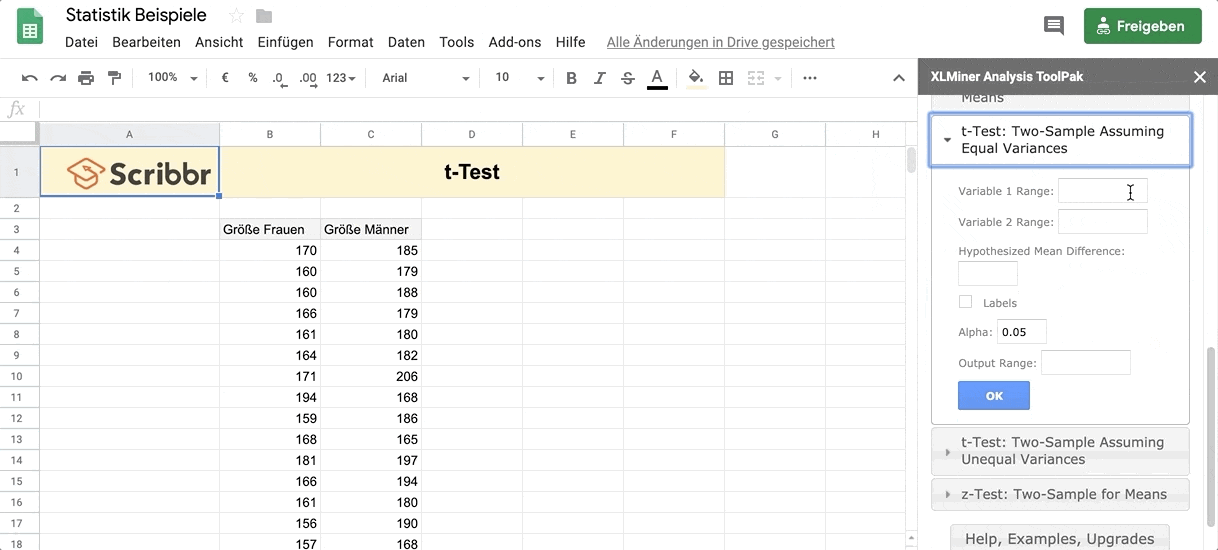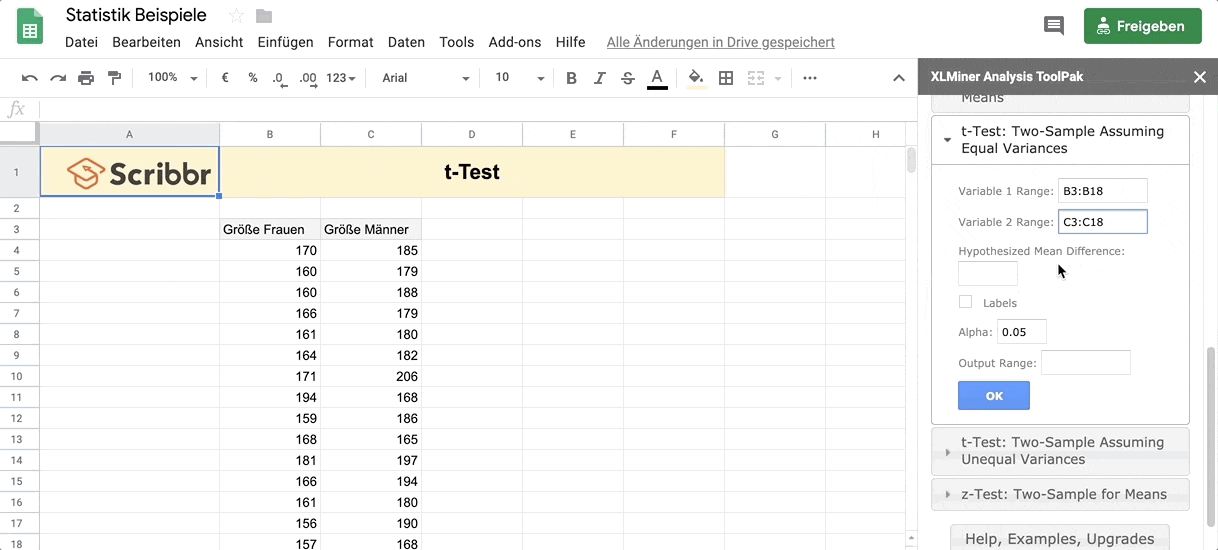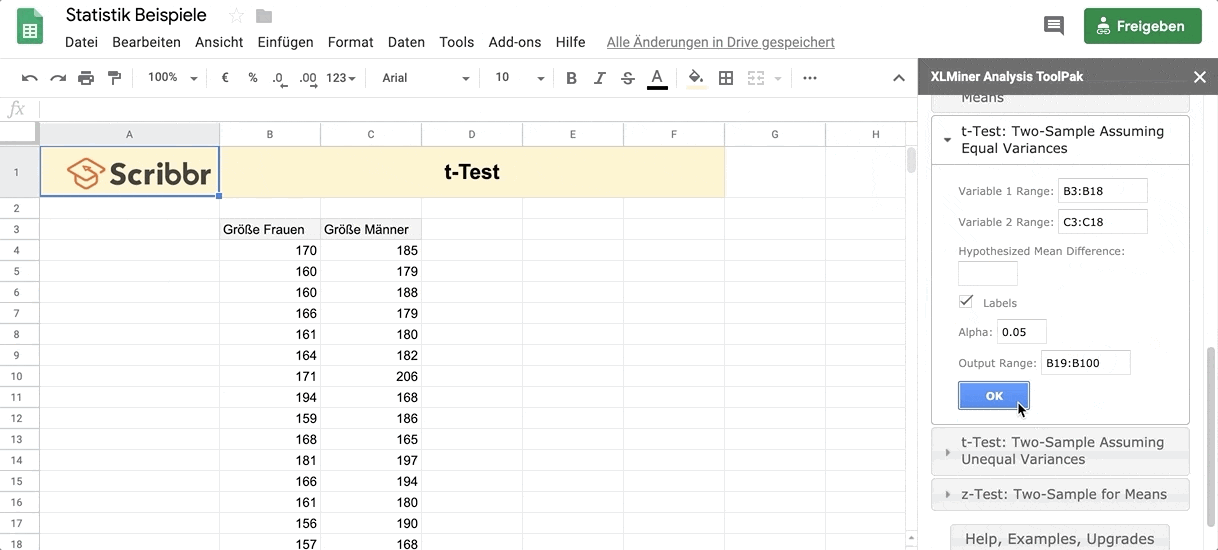
Variable 1 Range: Hier wählst du alle Daten zur Größe der Frauen aus (inklusive des Labels).
Variable 2 Range: Hier wählst du alle Daten zur Größe der Männer aus (inklusive des Labels).
Selektier Labels.
Output Range: Markier einen größeren Bereich im Arbeitsblatt unter den Datenfeldern, um dir die Ergebnisse des t-Tests anzeigen zu lassen.
Klick auf Ok, um den t-Test durchzuführen.
Ergebnisse des t-Tests interpretieren
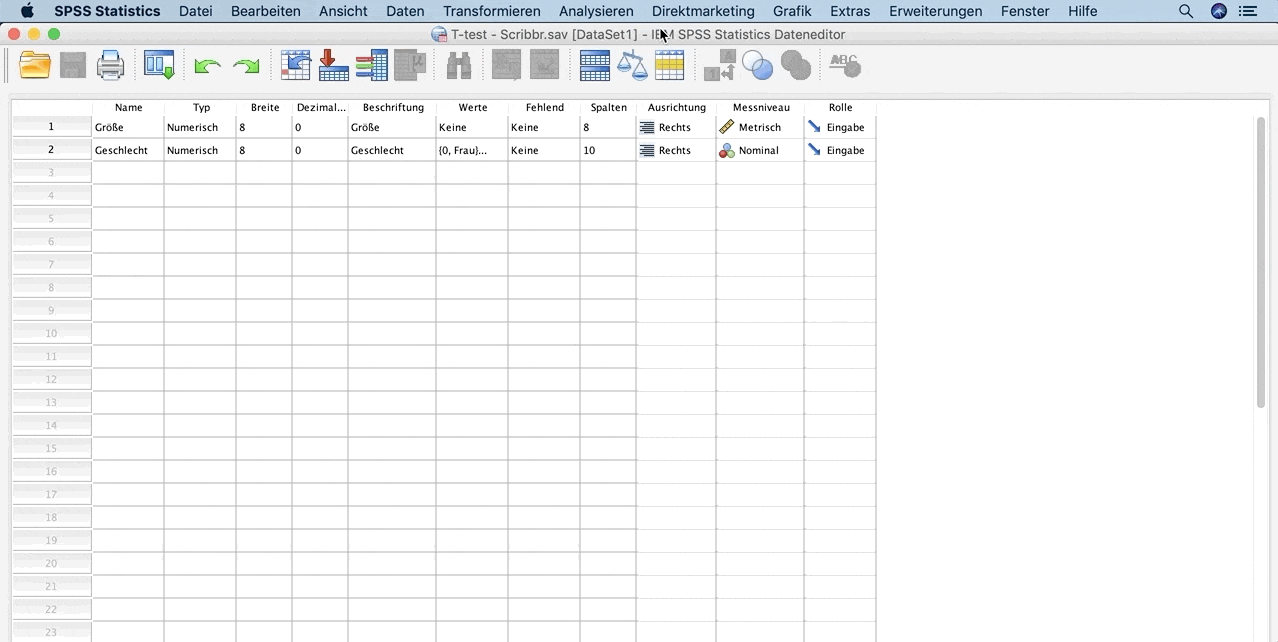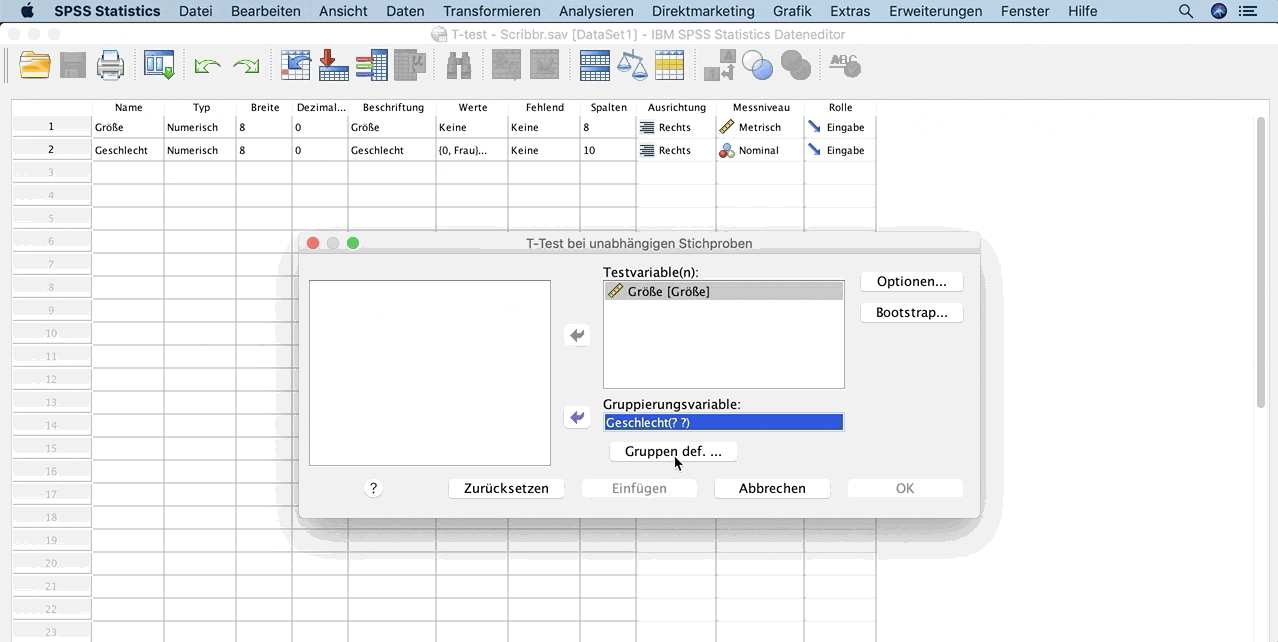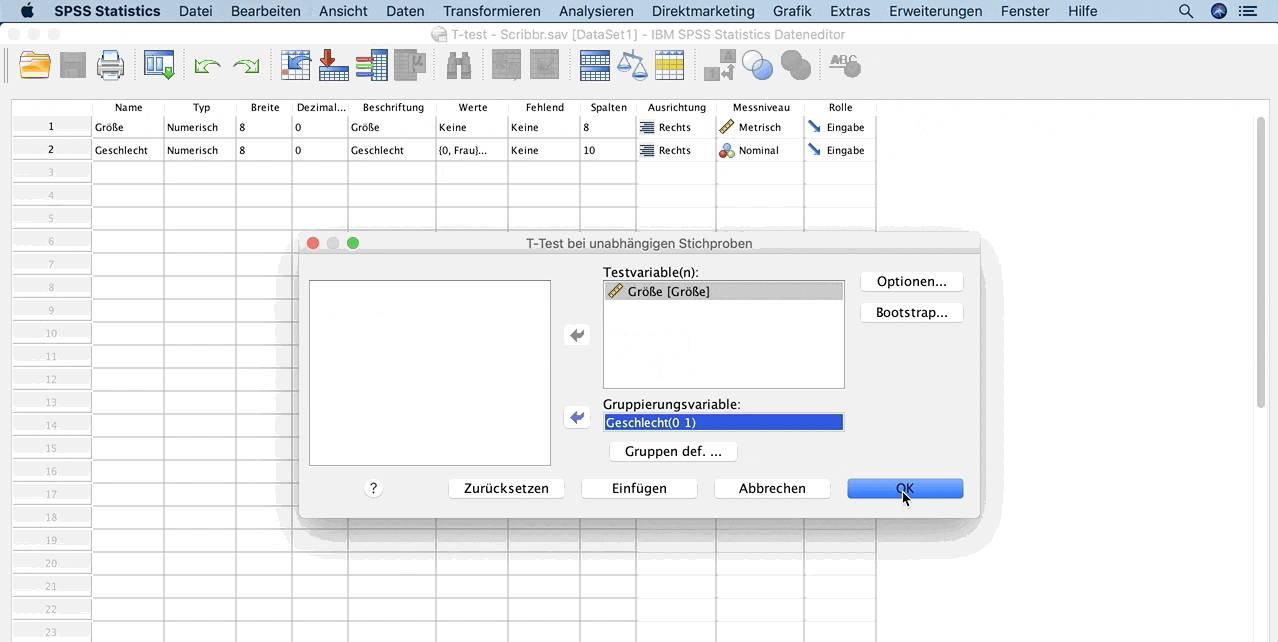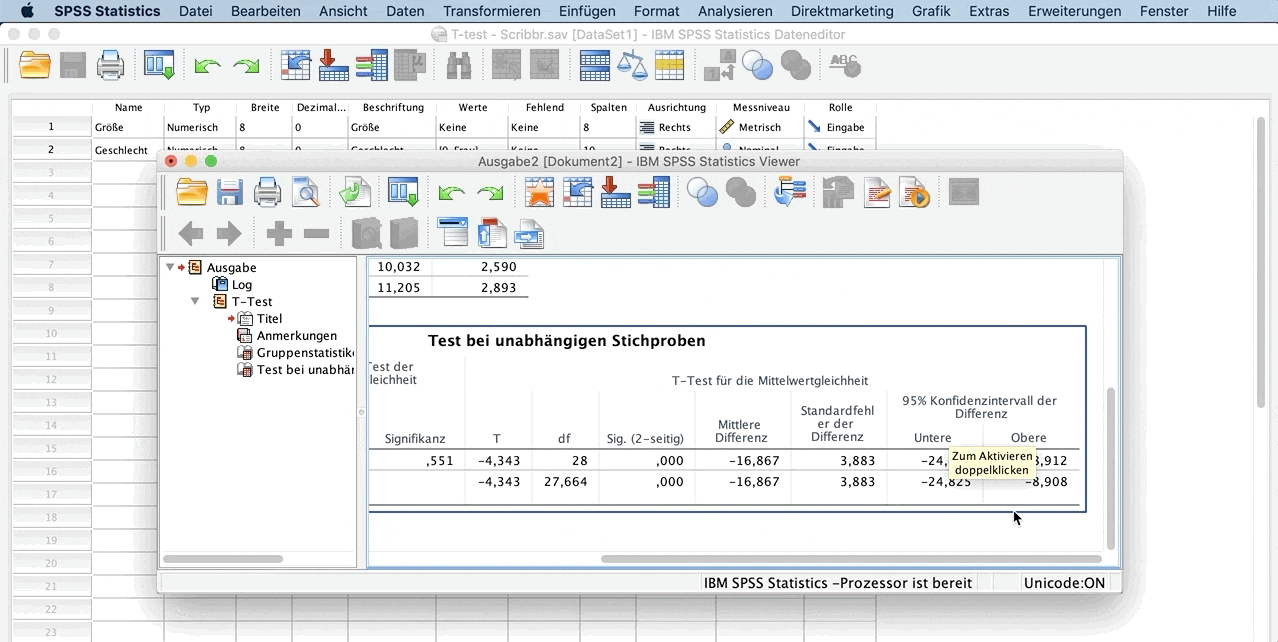
Die SPSS-Ausgabe für den unabhängigen Zweistichproben-t-Test beinhaltet zwei Tabellen.
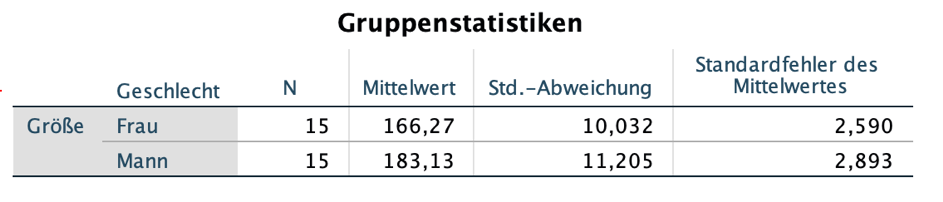
Gruppenstatistiken
Die erste Tabelle (Gruppenstatistiken) enthält deskriptive Statistiken zu beiden Gruppen, z. B. den Mittelwert, die Standardabweichung und den Standardfehler des Mittelwertes.
Test bei unabhängigen Stichproben
Die zweite Tabelle (Test bei unabhängigen Stichproben) zeigt das Ergebnis des t-Tests.
Levene-Test der Varianzgleichheit: Mit diesem Test kannst du analysieren, ob die Varianz beider Gruppen gleich ist. Das ist wichtig, um zu erkennen, ob du die erste oder letzte Zeile der Tabelle für deine Interpretation verwendest.
Signifikanz: Wenn die Signifikanz des Levene-Tests unter dem üblichen Wert von 0,05 liegt, wird die Nullhypothese (Die Varianzen sind gleich.) abgelehnt.
Für unsere Interpretation verwenden wir daher die Werte aus der ersten Reihe der Tabelle.
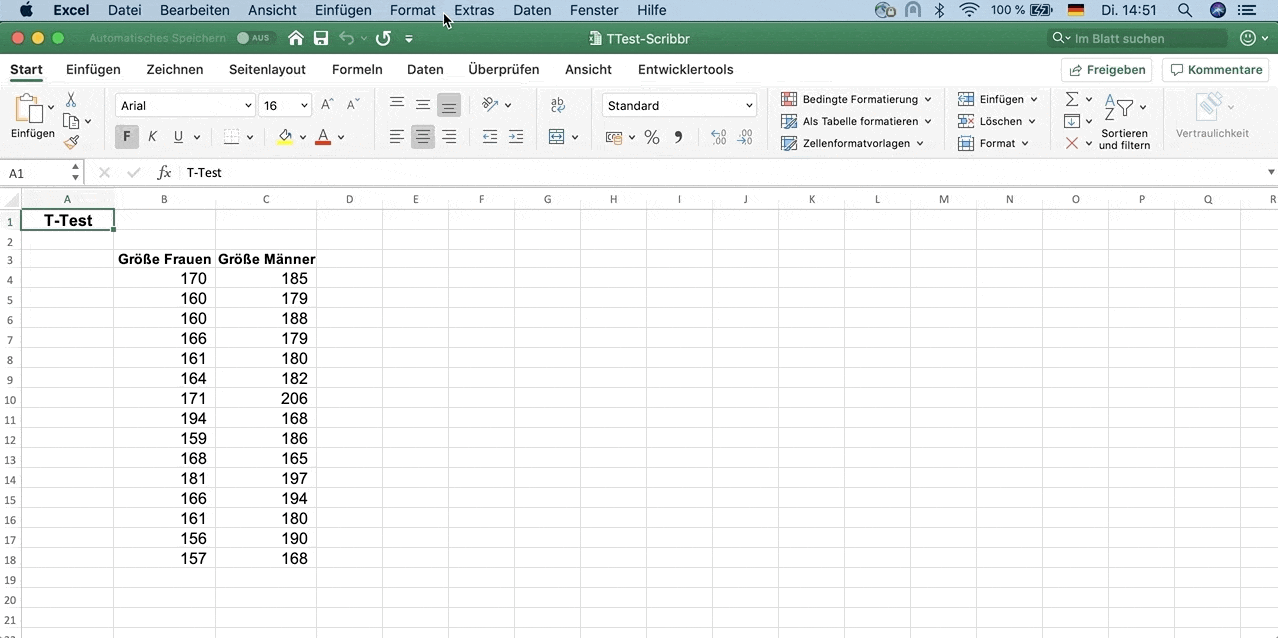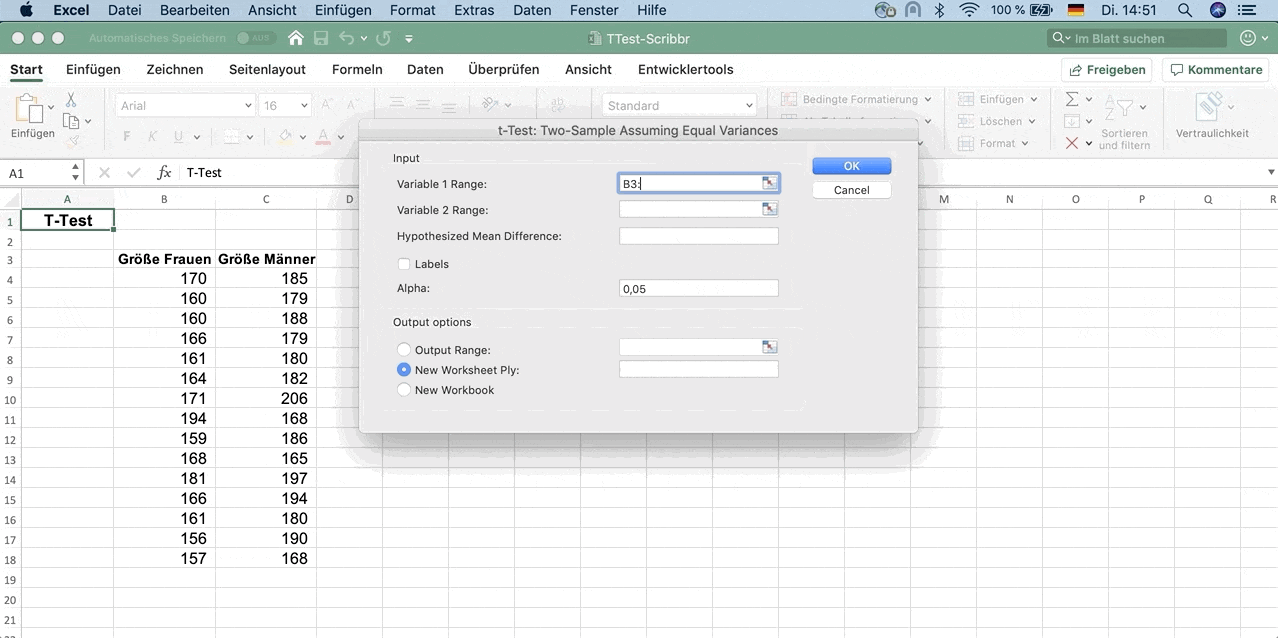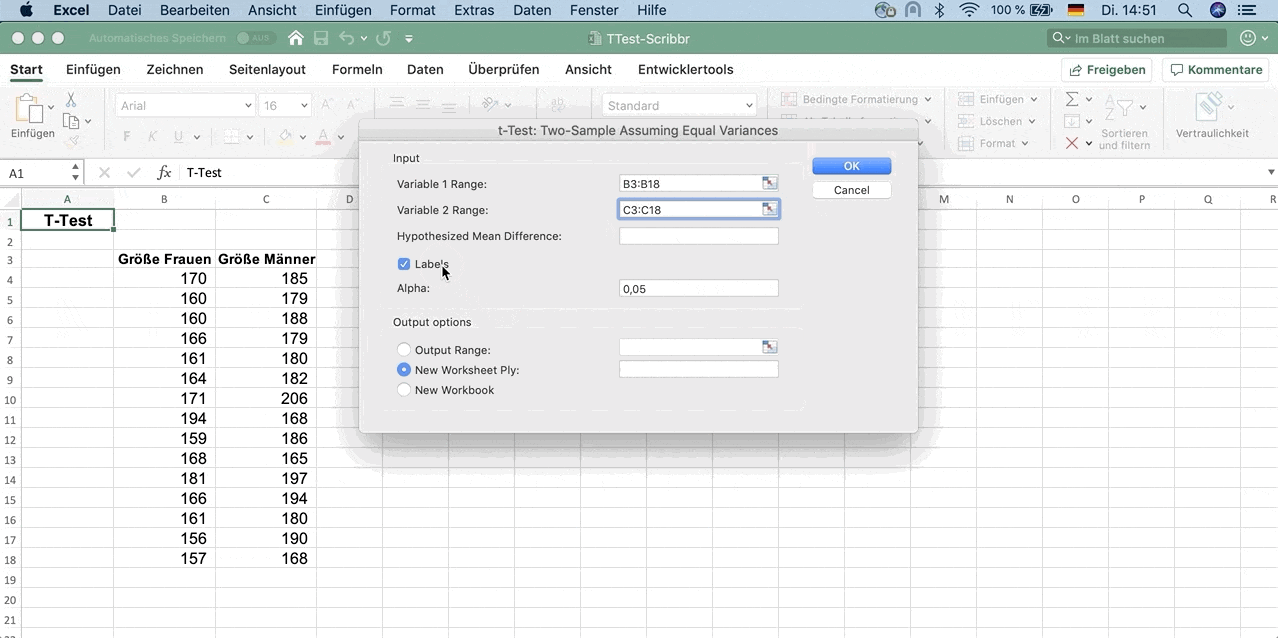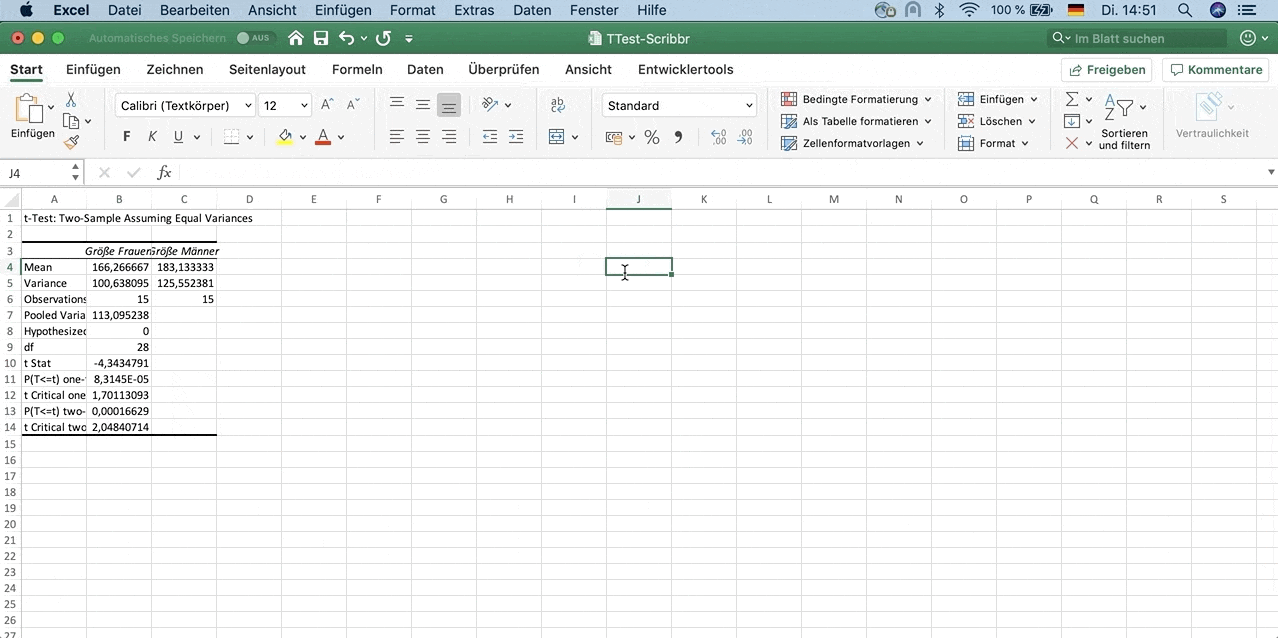
t-Wert: –4,434 mit den entsprechenden Freiheitsgraden (df = 28)
Sig. (2-seitig): Die Signifikanz wird mit 0,000 angegeben. Mit einem Sig.-Wert niedriger als 0,05 wird die Nullhypothese (Es gibt keine Unterschiede in den Mittelwerten.) verworfen.
Ergebnisse des t-Tests in deiner wissenschaftlichen Arbeit zusammenfassen
Du fasst die Ergebnisse deines t-Tests im Ergebniskapitel deiner Bachelorarbeit oder Masterarbeit zusammen.
Bei unabhängigen Stichproben (beim Zweistichproben-t-Test) solltest du dabei auf jeden Fall folgende Parameter angeben:
- Mittelwert und Standardabweichung für beide Gruppen,
- t-Wert mit der Anzahl der Freiheitsgrade und
- Signifikanz (Sig.) des t-Tests.
- Die Differenz zwischen der durchschnittlichen Größe von Frauen (M = 166,3; SD = 10,03) und jener von Männern (M = 183,1; SD = 11,21) war signifikant (t (28) = –4,34, p < 0,001).
- Die durchschnittliche Größe der Frauen (M = 166,3; SD = 10,03) war niedriger als die der Männer (M = 183,1; SD = 11,21). Die Differenz war sehr signifikant: t (28) = –4,34, p < 0,001.
Statistische Voraussetzungen für den t-Test
Bevor du einen t-Test durchführen kannst, sollten deine Daten bestimmte Bedingungen erfüllen.
Nur wenn diese Voraussetzungen erfüllt sind, liefert dein t-Test ein zuverlässiges Ergebnis:
- Die abhängige Variable ist intervall- oder ratioskaliert.
- Die Personen in den zwei Gruppen sind unabhängig voneinander. Du kannst dafür Zufallsstichproben verwenden.
- Wenn deine Stichprobe weniger als 30 Beobachtungen enthält, muss deine abhängige Variable normalverteilt sein.
Du kannst die Erfüllung dieser Bedingung in SPSS mit dem Shapiro-Wilk- oder dem Kolmogorov-Smirnov-Test überprüfen.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Flandorfer, P. (2023, 21. Juni). Den T-Test verstehen und interpretieren mit Beispiel. Scribbr. Abgerufen am 28. Juni 2025, von https://www.scribbr.de/statistik/t-test/