Statistische Korrelation berechnen und verstehen - mit Beispiel
Die Korrelation informiert uns über den Grad des Zusammenhangs zwischen zwei Variablen.
Dabei besagt eine positive Korrelation, dass sich die Variablen in die gleiche Richtung entwickeln. Wenn also eine Variable ansteigt, gilt dies auch für die andere Variable. Bei einer negativen Korrelation ist es gegenläufig: Ein Anstieg von Variable 1 bedeutet eine Abnahme von Variable 2.
Korrelationen richtig bestimmen und interpretieren
Die Korrelation wird mit dem Korrelationskoeffizienten angegeben. Dieser nimmt immer einen Wert zwischen -1 und +1 an.
Dabei besagt ein Korrelationskoeffizient…
- nahe der Zahl 1 → starke positive Korrelation,
z. B.: Größere Personen haben ein höheres Gewicht. - nahe der Zahl -1 → starke negative Korrelation
z. B.: Größere Personen haben ein geringeres Gewicht. - nahe der Zahl 0 → Es besteht kaum ein Zusammenhang zwischen den Variablen Größe und Gewicht.
Die Tabelle gibt dir eine Übersicht über die Entwicklungen der beiden Variablen je nachdem, ob sie positiv oder negativ korrelieren.
| Korrelation | Entwicklung der Variablen | Beispiel |
|---|---|---|
| Positive Korrelation | Variable 1 steigt → Variable 2 steigt | Steigt die Größe, steigt auch das Gewicht. |
| Variable 1 sinkt → Variable 2 sinkt | Sinkt die Größe, sinkt auch das Gewicht. | |
| Variable 2 steigt → Variable 1 steigt | Steigt das Gewicht, steigt auch die Größe. | |
| Variable 2 sinkt → Variable 1 sinkt | Sinkt das Gewicht, sinkt auch die Größe. | |
| Negative Korrelation | Variable 1 steigt → Variable 2 sinkt | Steigt die Größe, sinkt das Gewicht. |
| Variable 1 sinkt → Variable 2 steigt | Sinkt die Größe, steigt das Gewicht. | |
| Variable 2 steigt → Variable 1 sinkt | Steigt das Gewicht, sinkt die Größe. | |
| Variable 2 sinkt → Variable 1 steigt | Sinkt das Gewicht, steigt die Größe. |
Korrelation berechnen – Pearson oder Spearman?
Um die Korrelation zu berechnen und anzugeben, wird der Korrelationskoeffizient bestimmt. Dabei ist es vom Skalenniveau der Daten abhängig, welcher Korrelationskoeffizient der richtige ist.
Verwende den Korrelationskoeffizienten nach Pearson, wenn deine Daten metrisch sind, und den Rangkorrelationskoeffizienten nach Spearman, wenn du ordinale Daten vorliegen hast.
Korrelation mit dem Streudiagramm interpretieren
Zusätzlich zur Berechnung des Korrelationskoeffizienten kannst du ein Streudiagramm erstellen. Dieses veranschaulicht den Zusammenhang zwischen den zwei Variablen.
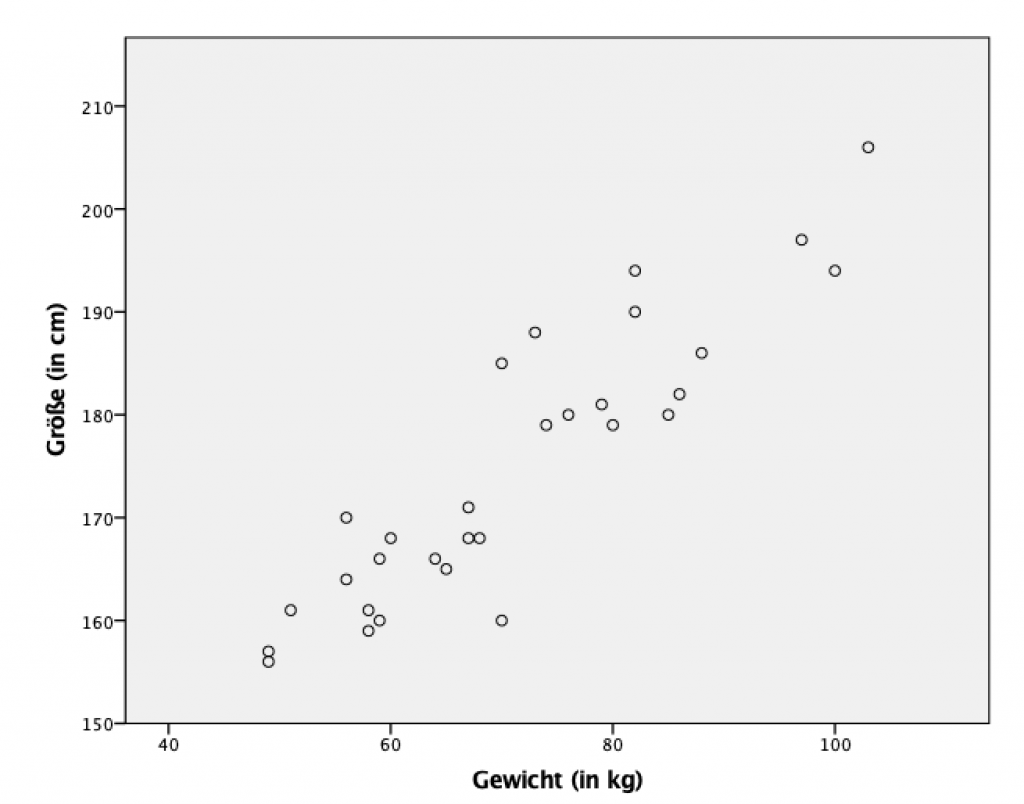
Die Abbildung zeigt das Streudiagramm zu unserem Beispiel mit der Größe und dem Gewicht von Personen. Wir sehen, dass eine positive Korrelation vorliegt, da die Verteilung der Beobachtungen (Punkte) eher einer Linie ähnelt.
Die Variablen entwickeln sich also in die gleiche Richtung und wir können schlussfolgern, dass eine höhere Größe mit einem höheren Gewicht einhergeht.
Streudiagramm in SPSS, Excel und Google Tabellen
Mit folgenden Schritten erstellst du ein Streudiagramm mit SPSS, Excel und Google Tabellen:
| SPSS | Grafik → Diagrammerstellung → Streu-/Punktdiagramm |
|---|---|
| Excel Google Tabellen |
Einfügen → Diagramm → Punkt (X, Y) bzw. Streudiagramm |
Korrelation und Kausalität
Bei der Bestimmung der Korrelation ist es wichtig zu beachten, dass die Korrelation zwar ein Hinweis, aber kein Beweis für einen kausalen Zusammenhang ist. Kausalität und Korrelation sind nicht dasselbe.
Dies zeigt das Beispiel von der Beobachtung der Störche und der Geburtenrate:
Wenn wir eine erhöhte Anzahl an Störchen beobachten und ebenfalls eine höhere Geburtenrate in der Region zu verzeichnen ist, können wir zwar sagen, dass eine Korrelation vorliegt, nicht aber, dass ein kausaler Zusammenhang besteht (z. B. dass der Storch die Babys bringt).
Wenn du herausfinden möchtest, ob es eine kausale Beziehung gibt, solltest du experimentelle Forschung oder eine Regressionsanalyse mit mehreren Kontrollvariablen durchführen.
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Häufig gestellte Fragen
- Was sagt die Korrelation aus?
-
Die Korrelation informiert uns über den Grad des Zusammenhangs zwischen zwei Variablen.
- Korrelationskoeffizient nach Pearson oder Spearman?
-
Verwende den Korrelationskoeffizienten nach Pearson bei metrischen Daten und den Rangkorrelationskoeffizienten nach Spearman bei ordinalen Daten, für die du eine Korrelation bestimmst.
- Bedeutet Korrelation Kausalität?
-
Nein, eine Korrelation ist zwar ein Hinweis, aber kein Beweis für einen kausalen Zusammenhang zwischen zwei Variablen.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2022, 11. November). Statistische Korrelation berechnen und verstehen - mit Beispiel. Scribbr. Abgerufen am 17. Dezember 2024, von https://www.scribbr.de/statistik/korrelation/
