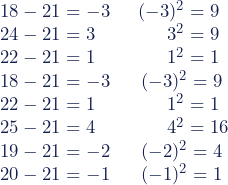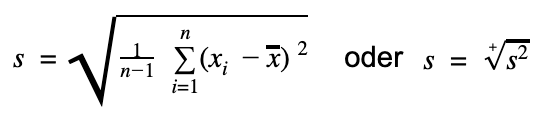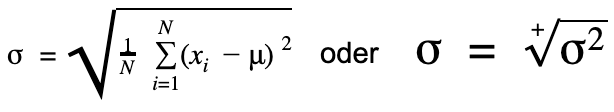Kostenlose Rechtschreibprüfung

Fehler kostenlos beheben

Kostenlose Plagiatsprüfung

Plagiate kostenlos finden

Korrektur deiner Abschlussarbeit

Fehler professionell beheben
  1. Home
  2. Wissensdatenbank
  3. Statistik
  4. Die Standardabweichung verstehen und berechnen + Rechner

Standardabweichung verstehen und berechnen + Rechner

Veröffentlicht am 25. März 2019 von Valerie Benning. Aktualisiert am 11. September 2023.

Die Standardabweichung ist ein Maß für die Streuung von Daten. Sie gibt an, in welchem Umfang erhobene Werte von ihrem Durchschnittswert abweichen.

Beispiel
Wir haben 5 Personen gefragt, wie viele Stunden Sport sie pro Woche treiben.

Person 1 2 3 4 5
Stunden Sport/Woche 2 3 7 5 3

Mittelwert:
\frac{2+3+7+5+3} {5}=4

Standardabweichung:
\sqrt{\frac{(2-4)^2+(3-4)^2+(7-4)^2+(5-4)^2+(3-4)^2}{5-1}}=\sqrt{\frac{4+1+9+1+1}{4}}=\sqrt{\frac{16}{4}}=2}

Die Standardabweichung in unserem Beispiel beträgt 2 Stunden.

Scribbrs kostenlose Rechtschreibprüfung
rechtschreibpruefung-allgemein

Fehler kostenlos beheben

Die Formeln zur Standardabweichung

Es gibt 2 Formeln für die Berechnung der Standardabweichung. Welche der beiden wir verwenden, hängt davon ab, ob wir die Standardabweichung einer Stichprobe oder einer Grundgesamtheit bestimmen wollen.

Formel zur Standardabweichung der Stichprobe
s=\sqrt{\frac{1}{n-1}\sum^n _{i=1}(x_i-\bar{x})^2}\,\,\,\,\,\, oder \,\,\,\,\,\, s=\sqrt[+]{s^2}
s Standardabweichung (der Stichprobe)
s^2 Varianz
n Gesamtzahl der Beobachtungen
x_i Beobachtungswert
\bar{x} arithmetisches Mittel (Mittelwert) der Stichprobe
Formel zur Standardabweichung der Grundgesamtheit
\sigma=\sqrt{\frac{1}{N}\sum^N _{i=1}(x_i-\mu)^2}\,\,\,\,\,\,oder\,\,\,\,\,\,\sigma=\sqrt[+]{\sigma^2}
\sigma Standardabweichung (der Grundgesamtheit)
\sigma^2 Varianz
N Gesamtzahl
x_i Beobachtungswert
\mu arithmetisches Mittel (Mittelwert) der Grundgesamtheit
Beachte
Wir verwenden n – 1, wenn wir die Daten einer Stichprobe vorliegen haben, und N, wenn es sich um eine Grundgesamtheit handelt. Da wir in unseren Beispielen die Standardabweichung einer Stichprobe bestimmen, verwenden wir die erste Formel.

Kostenlos auf Plagiate prüfen.

Plagiatsprüfung testen

Die Standardabweichung in 5 Schritten bestimmen

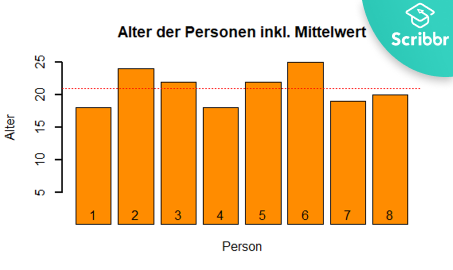
Nehmen wir an, wir haben acht Personen nach ihrem Alter gefragt und folgende Antworten erhalten:

Person 1 2 3 4 5 6 7 8
Alter 18 24 22 18 22 25 19 20

In der Abbildung sehen wir die Verteilung der verschiedenen Altersangaben der Personen. Die rote Linie zeigt das arithmetische Mittel des Alters in der Gruppe.
standardabweichung-berechnen-beispiel-altersverteilung-mit-mittelwert-scribbr

Allgemein Beispiel
1 Bestimme zunächst den Mittelwert x̄ deiner Beobachtungswerte. Wir berechnen den Mittelwert (x̄), indem wir alle Altersangaben addieren und dann die Summe durch die Gesamtanzahl der Personen teilen.

\bar{x}=\frac{18+24+22+18+22+25+19+20}{8}=\frac{168}{8}=21
2 Berechne nun die positive Abweichung der Beobachtungswerte vom Mittelwert.

Subtrahiere dazu den Mittelwert von den einzelnen Beobachtungswerten und quadriere das Ergebnis.

 Nun bestimmen wir die positiven Abweichungen der einzelnen Altersangaben vom Mittelwert x̄ = 21.

Dazu ziehen wir den Mittelwert von jeder Altersangabe ab und nehmen das Ergebnis zum Quadrat.

\\ 18-21&=-3\,\,\,\,\,\,\,\,\,(-3)^2=9 \\ 24-21&=3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3^2=9 \\ 22-21&=1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1^2=1 \\ 18-21&=-3\,\,\,\,\,\,\,\,\,\,(-3)^2=9 \\ 22-21&=1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1^2=1 \\ 25-21&=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4^2=16 \\ 19-21&=-2\,\,\,\,\,\,\,\,\,\,(-2)^2=4 \\ 20-21&=-1\,\,\,\,\,\,\,\,\,\,(-1)^2=1
3 Bilde nun die Summe aus den quadrierten Abweichungen. Wir addieren alle Ergebnisse aus Schritt 2.

9+9+1+9+1+16+4+1=50
4 Subtrahiere 1 von der Gesamtanzahl der Beobachtungen und teile die Summe aus Schritt 3 durch diese Zahl.

Als Ergebnis erhältst du die Varianz.

 Wir teilen das Ergebnis aus Schritt 3 durch 7, da wir insgesamt acht Personen nach dem Alter gefragt haben.

\\ 8-1&=7 \\ \frac{50}{7}&=7.14 [Jahre^2]
5 Ziehe die Wurzel aus der Varianz.

Als Ergebnis erhältst du die Standardabweichung.

 Wir ziehen die Wurzel aus der Varianz, also aus dem Ergebnis aus Schritt 4.

\sqrt{7.14}=2.67

Die Standardabweichung vom durchschnittlichen Alter (21 Jahre) beträgt 2.67 Jahre.
Merke
Die Standardabweichung erhältst du, indem du die Wurzel aus der Varianz ziehst.

Standardabweichung berechnen mit Standardabweichung Rechner

Du kannst die Standardabweichung von Hand oder mithilfe unseres Standardabweichung Rechners berechnen.

Standardabweichung berechnen mit Excel und Google Tabellen

Standardabweichung Excel

Excel

Standardabweichung Google Tabellen

Google Tabellen

Mit unserer Excel-Datei oder der Google Tabellen-Datei kannst du die Standardabweichung ganz einfach selbst berechnen.

Unter den Daten zum Alter gibst du in der leeren Zelle

  • in Excel die Formel =STABW.S() ein
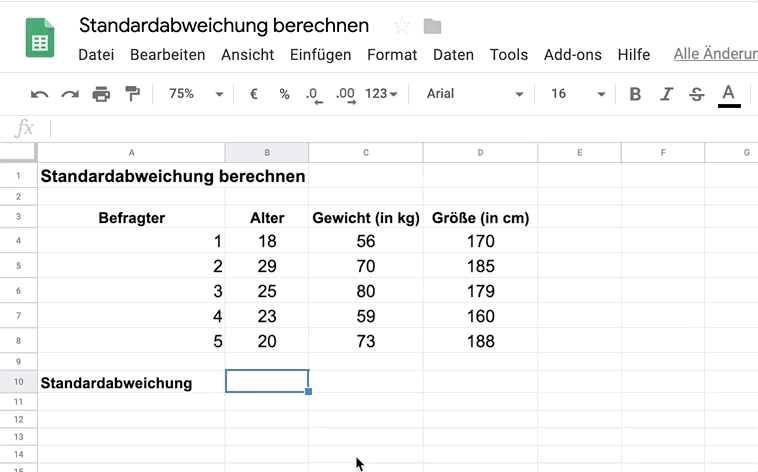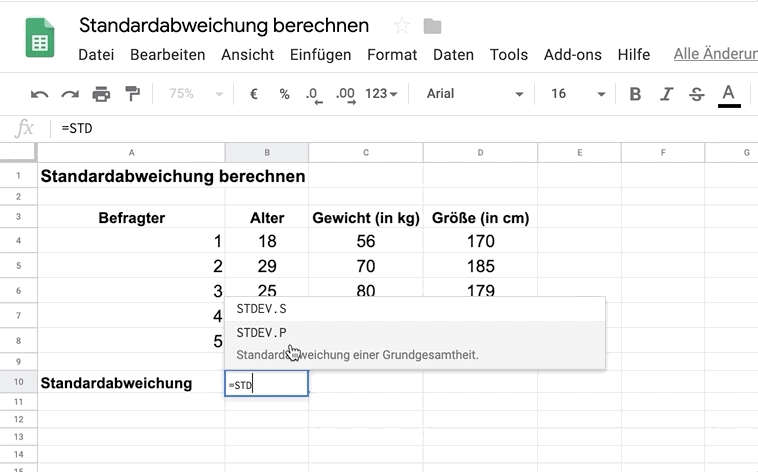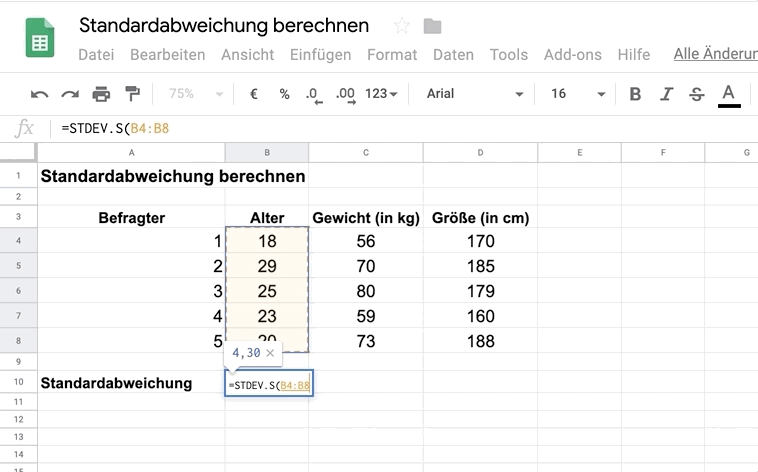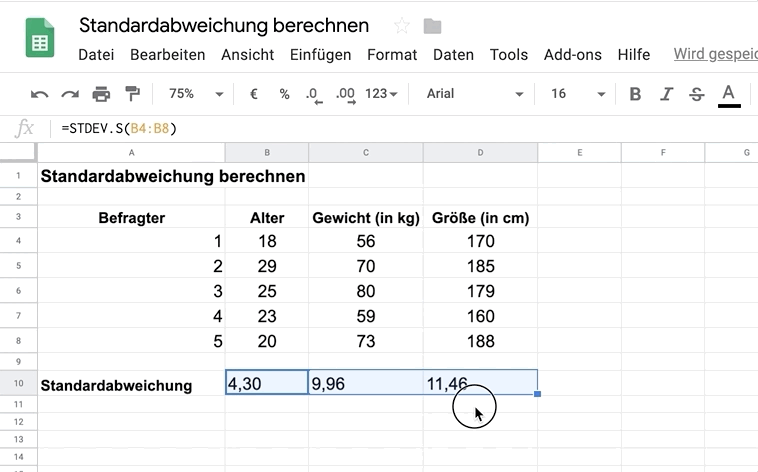
  • in Google Tabellen die Formel =STDEV.S() ein

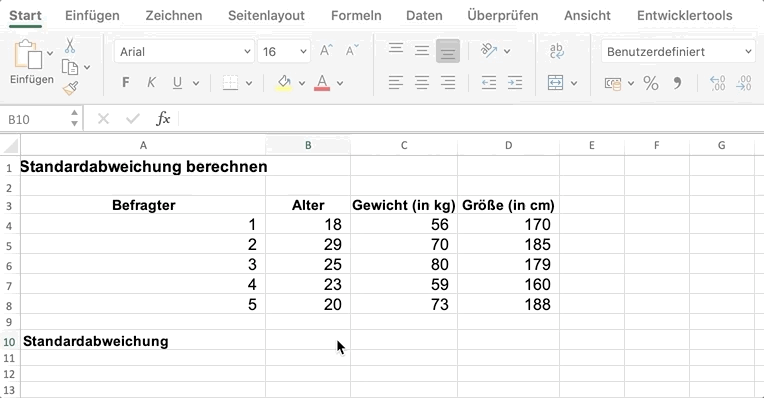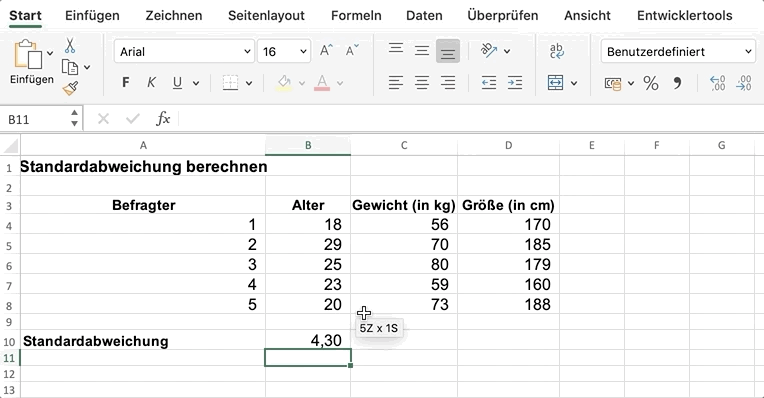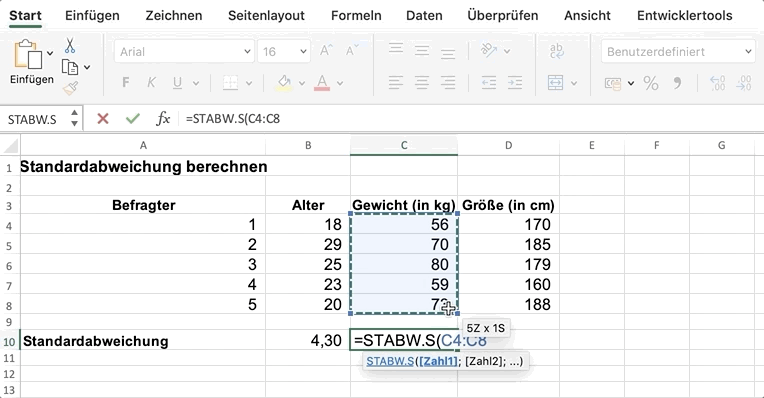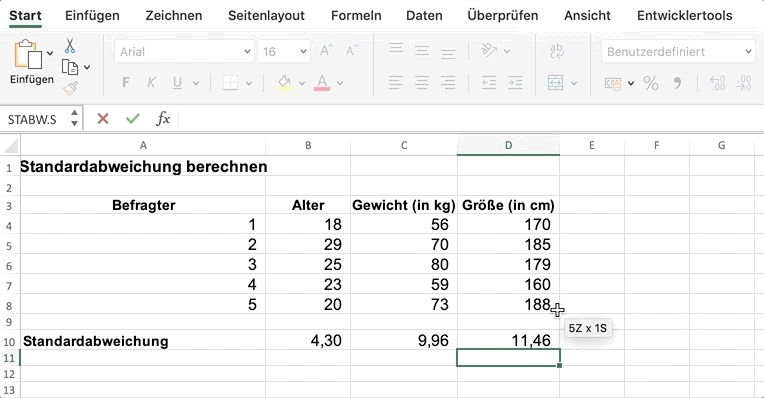
In die Klammern fügen wir die Zellen mit den Altersangaben der Befragten ein. Als Ergebnis erhältst du die Standardabweichung 4,30.

Du kannst nun dasselbe für die Werte Gewicht und Größe wiederholen.

Das ‚.S‘ nach ‚STABW‘ informiert Excel, dass es sich um eine Stichprobe handelt, für welche die Standardabweichung berechnet werden soll.

Möchtest du eine fehlerfreie Arbeit abgeben?

Mit einem Lektorat helfen wir dir, deine Abschlussarbeit zu perfektionieren.

Neugierig? Bewege den Regler von links nach rechts!

Zu deiner Korrektur

Standardabweichung berechnen mit SPSS

Standardabweichung SPSS

SPSS

Mit unserer SPSS-Datei kannst du die Berechnung der Standardabweichung selbst üben.

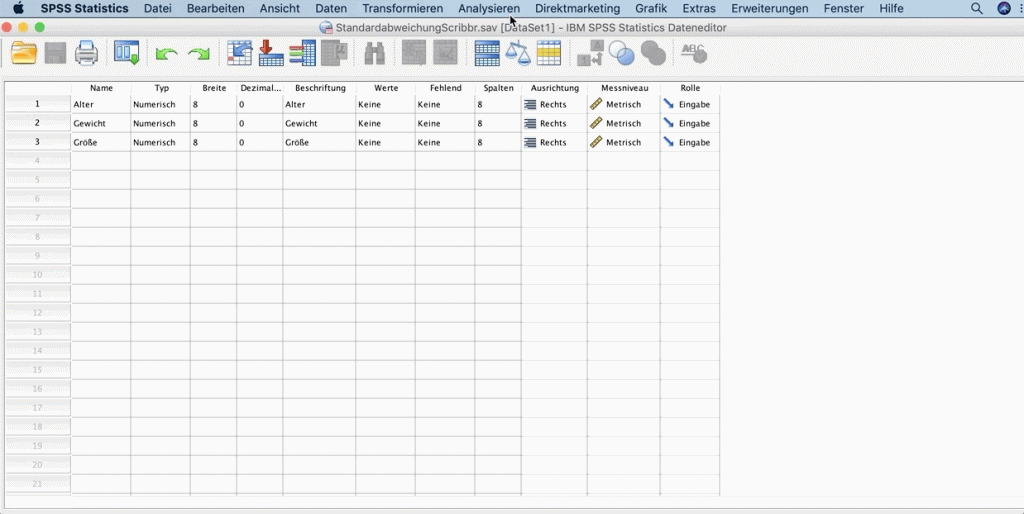
Um die Standardabweichung mit SPSS zu berechnen, klicke im Menü auf Analysieren → Deskriptive Statistiken → Deskriptive Statistik.

Im Fenster wählst du die Variablen Alter, Gewicht und Größe aus.

Danach klickst du auf Optionen und wählst Standardabweichung aus. Mit Weiter und Ok führst du die Analyse durch.

Ergebnisse der Standardabweichung zusammenfassen

Wenn du in deiner Bachelorarbeit bzw. Masterarbeit deine Stichprobe beschreiben möchtest, wirst du statistische Kennzahlen wie den Mittelwert und die Standardabweichung verwenden. Du informierst damit die Leserschaft über die Eigenschaften der Stichprobe der Befragten.

Beispiel Ergebnisse in der Abschlussarbeit zusammenfassen
Das durchschnittliche Alter der befragten Studierenden beträgt 23 Jahre mit einer Standardabweichung von 4,30 Jahren (M = 23; SD = 4,30).
Beachte
Die Abkürzungen M für Mittelwert und SD für Standardabweichung werden kursiv geschrieben. Um die beiden Werte voneinander zu trennen, verwendest du einen Strichpunkt.

Häufig gestellte Fragen

Was ist die Standardabweichung?

Die Standardabweichung ist ein Maß für die Streuung von Daten. Sie gibt die durchschnittliche Abweichung aller erhobenen Werte von ihrem Durchschnittswert an.

Was sagt die Standardabweichung aus?

Die Standardabweichung sagt aus, in welchem Umfang Werte in einem Datensatz von ihrem Durchschnittswert abweichen.

Was ist xi bei der Standardabweichung?

xi in der Formel der Standardabweichung ist dein Beobachtungswert.

Beispiel
Du hast 20 Personen nach dem Alter gefragt und möchtest nun die Standardabweichung des Alters in der Gruppe bestimmen. Füge für xi die einzelnen Altersangaben der Personen in die Formel der Standardabweichung ein.
Wie berechnet man die Standardabweichung?

Welche Formel du zur Berechnung der Standardabweichung verwendest, hängt davon ab, ob du die Daten einer Stichprobe oder einer Grundgesamtheit vorliegen hast.

Formeln zur Standardabweichung
Stichprobe Grundgesamtheit
standardabweichung-der-stichprobe-formel-scribbr standardabweichung-der-grundgesamtheit-formel-scribbr
Beachte
Wenn du die Varianz bereits gegeben hast, kannst du die Standardabweichung auch bestimmen, indem du die Wurzel aus der Varianz ziehst.
Beispiel
wie-berechnet-man-die-standardabweichung-beispiel-scribbr
Wie berechnet Excel die Standardabweichung?

Gib in Excel =STABW.S() oder =STDEV.S() ein, um die Standardabweichung einer Stichprobe zu bestimmen. In die Klammern schreibst du dann die Zellen mit den Werten, für die du die Standardabweichung bestimmen willst.

Beispiel
Deine Werte, für die du die Standardabweichung bestimmen willst, stehen in den Zellen C3 bis L3. Schreibe also in eine leere Zelle: =STABW.S(C3:L3) oder =STDEV.S(C3:L3) und du erhältst die Standardabweichung der Werte in diesen Zellen.

Beachte dabei, dass es sich um die Standardabweichung einer Stichprobe handelt. Die Standardabweichung einer Grundgesamtheit kannst du in Excel mit dem Befehl =STABW.N. bestimmen.

Diesen Scribbr-Artikel zitieren

Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.

Benning, V. (2023, 11. September). Standardabweichung verstehen und berechnen + Rechner. Scribbr. Abgerufen am 18. November 2024, von https://www.scribbr.de/statistik/standardabweichung/

Diesen Artikel zitieren
War dieser Artikel hilfreich?
Valerie Benning

Hi, ich bin Valerie und schreibe zur Zeit selbst meine Masterarbeit in Psychologie. Meine Erfahrungen aus dem Studium teile ich gerne, damit Studierenden statistische Themen leichter fallen.

Das hat anderen Studierenden noch gefallen

Abstract Beispiel für eine Bachelorarbeit oder Masterarbeit

Dieses Beispiel des Abstracts einer Bachelorarbeit kann für das Schreiben deiner (Management)-Zusammenfassung als Leitfaden genommen werden.
261

Signifikanzniveau einfach erklärt mit Beispiel

Das Signifikanzniveau α beschreibt die maximale Wahrscheinlichkeit, dass eine Nullhypothese fälschlicherweise abgelehnt wird.
467

Beispiele für wissenschaftliche Arbeiten - Hausarbeit, Bachelorarbeit und mehr

Nutze unsere wissenschaftliche Arbeit Beispiele als Inspiration für deine eigene Hausarbeit, Bachelorarbeit, Masterarbeit und mehr.
49