Den Modus verstehen und bestimmen + Modus Rechner
Der Modus ist der Wert, der in einem Datensatz am häufigsten vorkommt.
Unter all deinen Beobachtungsdaten ist der Modus also die Beobachtung, die du am häufigsten gemacht hast.
Eine andere Bezeichnung für den Modus ist auch der Modalwert.
| Note | sehr gut | gut | befriedigend | ausreichend | mangelhaft | ungenügend |
|---|---|---|---|---|---|---|
| Häufigkeit | 3 | 7 | 5 | 5 | 1 | 0 |
Modus: gut
Der Modus in dem Beispiel ist die Note gut. Diese wurde sieben Mal vergeben und ist damit die Note, die am häufigsten vorkommt.
Den Modus können wir bereits bestimmen, wenn wir nominale Daten haben, zum Beispiel die Haarfarbe, das Geschlecht, der Geburtsort oder die Postleitzahl.
Nominale Daten können wir nicht in eine Rangreihenfolge bringen. Dies bedeutet, dass wir nicht sagen können, dass ein Wert besser oder schlechter als ein anderer ist, sondern nur, ob es einen Unterschied gibt.
Modus Rechner
Du kannst den Modus von Hand oder mithilfe unseres Modus Rechners berechnen.
Den Modus bestimmen
Wir können den Modus einfach bestimmen, indem wir uns die Häufigkeiten der einzelnen Beobachtungswerte anschauen und den Wert ablesen, der am häufigsten beobachtet wurde.
Der Modus wird auch geschrieben als x̄d.
Dabei gilt: x̄d = häufigster Beobachtungswert.
Für unser Beispiel zur Notenverteilung können wir also auch schreiben: x̄d = gut.
| Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Lieblingsfarbe | Rot | Grün | Grün | Gelb | Rot | Grün | Blau | Rot |
|
Häufigkeiten |
|||
|---|---|---|---|
| Blau | Grün | Rot | Gelb |
| 1 | 3 | 3 | 1 |
Modus: Grün und Rot
Grün und Rot treten beide dreimal und damit am häufigsten auf. Daher haben wir in diesem Beispiel zwei Modi.
Der Modus in der Statistik an Beispielen erklärt
Der Modus kann für jedes Skalenniveau angewandt werden.
Wir können den Modus also bestimmen, wenn wir zum Beispiel Personen nach ihrer Augenfarbe gefragt haben (Nominalskala), uns die Notenverteilung einer Klausur anschauen (Ordinalskala) oder über mehrere Tage die Temperatur gemessen haben (Intervallskala).
Wir haben 10 Personen nach ihrer Augenfarbe gefragt und folgende Antworten erhalten.
| Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Augenfarbe |
Braun |
Grün | Grün |
Braun |
Blau |
Braun |
Blau | Grün |
Braun |
Braun |
|
Häufigkeiten |
||
|---|---|---|
| Blau | Grün |
Braun |
| 2 | 3 | 5 |
Ergebnis
x̄d = Braun
Der Modus ist Braun, da diese Augenfarbe am häufigsten unter den Personen vorkommt.
Die folgende Tabelle zeigt wie häufig die einzelnen Klausurnoten in einer Klasse auftreten.
| Note | sehr gut | gut | befriedigend | ausreichend | mangelhaft | ungenügend |
|---|---|---|---|---|---|---|
| Häufigkeit | 3 | 7 | 5 | 5 | 1 | 0 |
Ergebnis
x̄d = gut
Der Modus ist die Note gut, da diese am häufigsten in der Klasse vorkommt.
Wir haben eine Woche lang die Temperatur gemessen und folgende Werte erhalten.
| Tag | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Temperatur in °C | 22 | 25 | 18 | 22 | 20 | 21 | 19 |
Ergebnis
x̄d = 22
Der Modus beträgt 22°C, da diese Temperatur am häufigsten in der Woche gemessen wurde.
Vergleich zu Median und zum arithmetischen Modus
Wie auch der Median und das arithmetische Mittel gehört der Modus zu den Lageparametern.
In der deskriptiven Statistik verwenden wir Lageparameter, um die zentrale Lage einer Verteilung von Daten anzugeben, also zum Beispiel den Mittelwert oder den Zentralwert.
Den Modus können wir auch anwenden, wenn wir nominale Daten haben, zum Beispiel die Augenfarbe. Dies ist bei anderen Lageparametern nicht der Fall.
Für den Median und das arithmetische Mittel benötigen wir mindestens ordinalskalierte Daten, das heißt, wir müssen die Daten in eine Rangreihenfolge bringen können.
Auch in deiner Bachelorarbeit oder Masterarbeit kannst du Lageparameter für statistische Auswertungen verwenden.
Nehmen wir an, wir haben 20 Menschen nach ihrem Alter gefragt und folgende Werte erhalten:
| Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alter | 18 | 20 | 21 | 21 | 21 | 23 | 25 | 25 | 25 | 25 | 26 | 27 | 27 | 29 | 29 | 30 | 30 | 32 | 34 | 88 |
| Erklärung | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beim Modus bestimmen wir, welcher Wert in unseren Beobachtungsdaten am häufigsten vorkommt. | ||||||||||||||||||||||||||
| Berechnung | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| Ergebnis | ||||||||||||||||||||||||||
| Am häufigsten kommt ein Alter von 25 Jahren in der Gruppe vor. |
| Erklärung |
|---|
| Beim Median bestimmen wir, welcher Wert genau in der Mitte der geordneten Reihe aller Beobachtungsdaten liegt und diese in zwei Hälften teilt. |
| Berechnung |
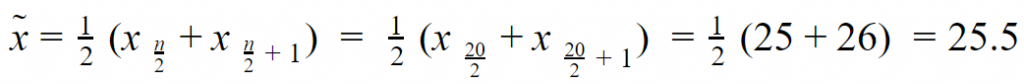 |
| Ergebnis |
| Ein Alter von 25.5 Jahren teilt die Gruppe in zwei Hälften. |
| Erklärung |
|---|
| Beim arithmetischen Mittel bestimmen wir den durchschnittlichen Wert aller Beobachtungsdaten. |
| Berechnung |
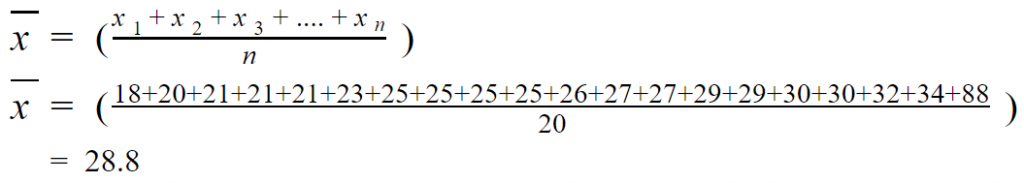 |
| Ergebnis |
| Im Durchschnitt sind die Personen in der Gruppe 28.8 Jahre alt. |
Um deine statistischen Ergebnisse zu interpretieren, solltest du auch Streuungsmaße, wie Standardabweichung, Spannweite oder Varianz, verwenden.
Häufig gestellte Fragen
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2023, 02. Mai). Den Modus verstehen und bestimmen + Modus Rechner. Scribbr. Abgerufen am 9. Juli 2025, von https://www.scribbr.de/statistik/modus/