Die Standardnormalverteilung verstehen + Rechner

Die Standardnormalverteilung ist eine besondere Form der Normalverteilung und wird daher ebenfalls verwendet, um Häufigkeiten von Daten und Beobachtungen darzustellen.

Eine Standardnormalverteilung liegt immer dann vor, wenn wir eine Normalverteilung mit einem Mittelwert von = 0 und einer Standardabweichung von  = 1 haben.

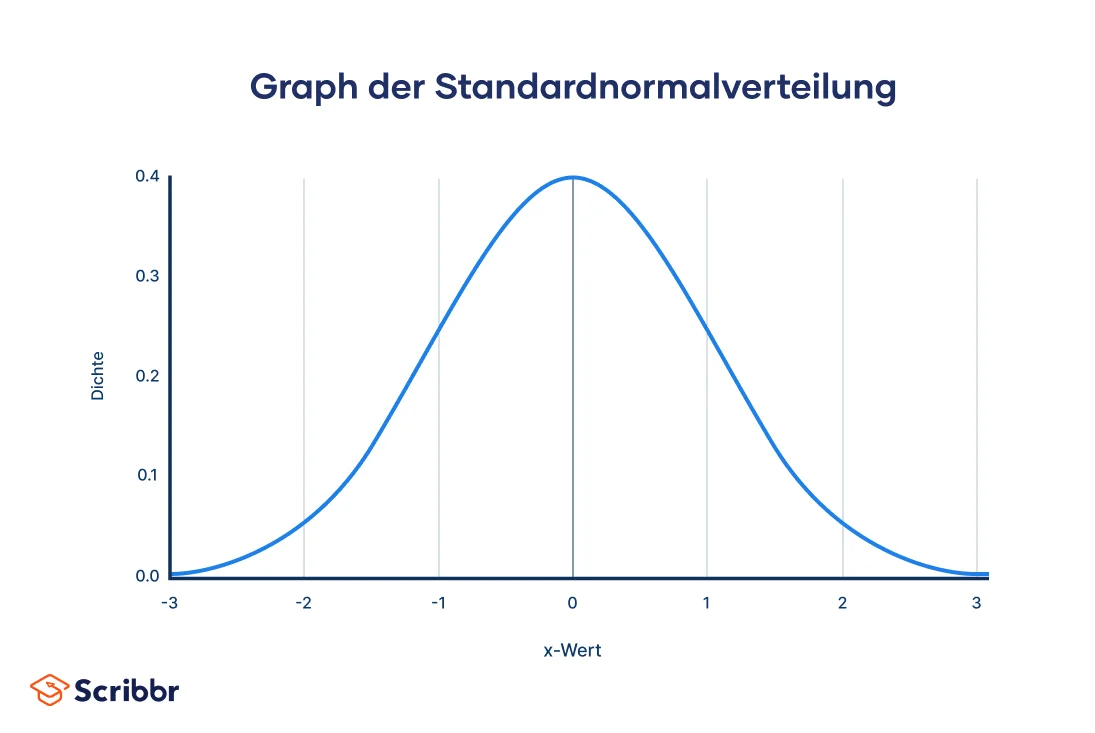
Hier siehst du den Graphen zur Standardnormalverteilung. Wir können direkt den Mittelwert von = 0 erkennen.

Standardnormalverteilung Rechner

Du kannst die Standardnormalverteilung mithilfe unseres Standardnormalverteilung Rechner berechnen.

Von der Normalverteilung zur Standardnormalverteilung

Bei Normalverteilungen können sich die Werte für den Erwartungswert μ und die Standardabweichung σ je nach Kontext unterscheiden. Daher gibt es unendlich viele mögliche Normalverteilungen.

Um mit den Daten weiterarbeiten zu können, müssen wir zunächst unsere Normalverteilung in die Standardnormalverteilung transformieren.

Dies ist mit jeder Normalverteilung möglich und wird auch Standardisierung genannt, denn wir berechnen aus unseren Daten einen standardisierten z-Wert.

Die Standardisierung ist notwendig, damit wir anschließend die Tabelle der Standardnormalverteilung verwenden können. In dieser können wir anhand des z-Werts die Wahrscheinlichkeit für einen bestimmten Wert in dem Datensatz ablesen.

Formel zur Standardisierung
	standardnormalverteilte Zufallsvariable z
	Zufallsvariable
	Erwartungswert
	Standardabweichung

Bei der Standardisierung entnehmen wir den Einfluss der Lage (Mittelwert) und der Verteilung (Standardabweichung) der ursprünglichen Verteilung.

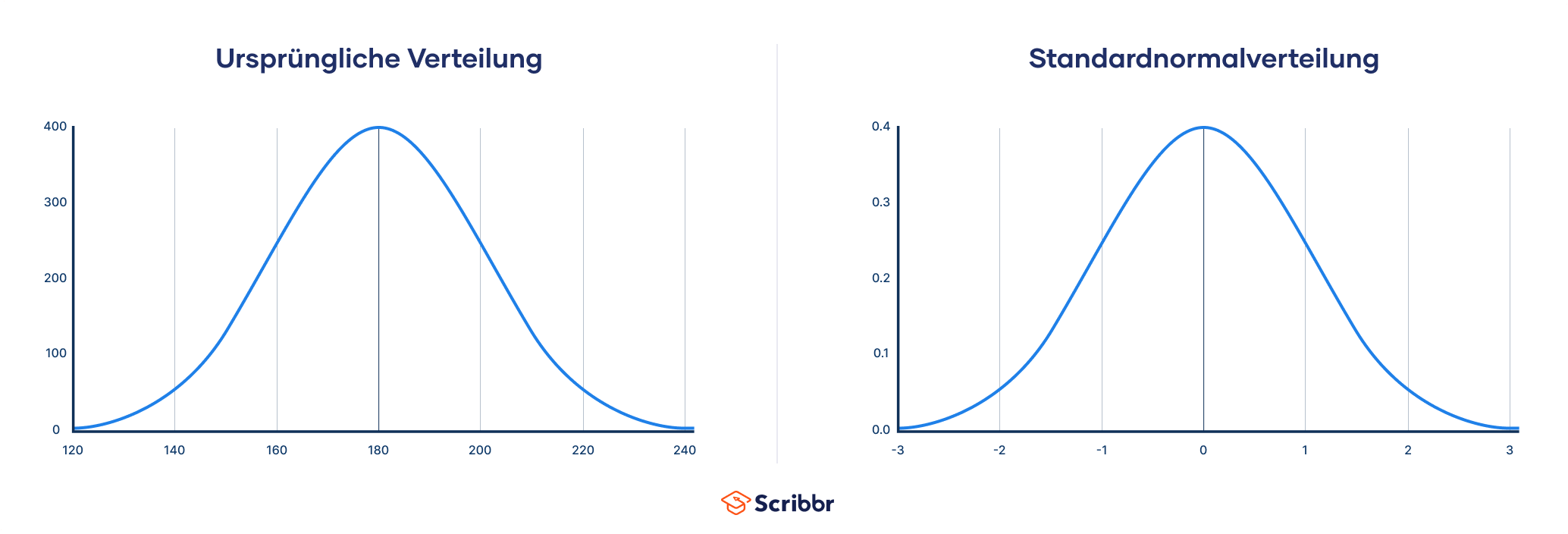
Was das genau bedeutet, zeigen die beiden Abbildungen.

Links sehen wir die ursprüngliche Verteilung in unserem Datensatz mit einem Mittelwert von μ = 180 cm und einer Standardabweichung von σ = 10 cm.

Der rechte Graph gehört zur Standardnormalverteilung und hat einen Mittelwert von μ = 0 und eine Standardabweichung von σ = 1. Wir sehen, dass die Einheit (Zentimeter) und die ursprünglich gemessenen Körpergrößen nun keinen Einfluss mehr auf den Verlauf des Graphen haben.

Transformation in die Standardnormalverteilung am Beispiel erklärt

Wir haben die Körpergröße von 5000 zufällig ausgewählten Personen in einer Stadt gemessen und berechnet, dass der Mittelwert bei = 1.80 m und die Standardabweichung bei = 10 cm liegt.

Nun wollen wir die Wahrscheinlichkeit bestimmen, dass eine Person in der Stadt kleiner als zwei Meter groß ist.

Dies können wir auch schreiben als: P(x < 200). Dabei steht x für unseren gesuchten Wert und P für die Wahrscheinlichkeit, dass dieser zutrifft.

Für die Berechnung der Wahrscheinlichkeit müssen wir zunächst die ursprüngliche Verteilung in die Standardnormalverteilung transformieren.

Dazu verwenden wir die folgenden 5 Schritte zur Standardisierung.

Schritt-für-Schritt-Erklärung zur Standardisierung

1	Schaue zunächst, welche Daten du vorliegen hast. Solltest du die Varianz gegeben haben, gilt auch hier wieder, die Wurzel zu ziehen, um die Standardabweichung zu erhalten. Achte auch darauf, dass alle Parameter die gleiche Einheit haben.	= 100 = 10 = 1.80 m = 180 cm (Alternativ kannst du natürlich auch = 10 cm in =  0.1 m umrechnen.)
2	Setze die Werte in  ein.
3	Für den z-Wert aus Schritt 2 kannst du nun in der Tabelle der Standardnormalverteilung die zugehörige Wahrscheinlichkeit ablesen. Die Tabelle findest du am Ende dieses Artikels.	Aus der Tabelle ist zu entnehmen, dass = 2.0 = 0.9772.
4	Nun kannst du die Wahrscheinlichkeit berechnen indem du den Wert aus Schritt 3 mit 100 multiplizierst.	0.9772 * 100 = 97.72 %
5	Als letzten Schritt kannst du das Ergebnis formulieren.	Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person kleiner als 2.00 m groß ist, beträgt 97.72 %.

Beispielrechnungen mit Lösung

Für die Beispiele schauen wir uns weiterhin die Verteilung der Körpergröße in der Stadt an.

Zur Erinnerung:

• Standardabweichung = 10 cm
• Erwartungswert = 1.8m = 180 cm

Schritt 1: Parameter vorbereiten.	= 10 cm = 180 cm = 200 cm Gesucht: P(x > 200)
Schritt 2: Werte in  einsetzen.
Schritt 3: z-Wert aus Schritt 2 in Tabelle der Standardnormalverteilung ablesen.	= 2.00 = 0.9772
Schritt 4: Wahrscheinlichkeit berechnen.	Da wir nun die Wahrscheinlichkeit berechnen, dass eine Person größer als 2.00m ist, müssen wir rechnen: P = 1 – 0.9772 = 0.0228. P = (1– 0.9772) * 100 = 2.28 %
Schritt 5: Ergebnis formulieren.	Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person größer als 2 m ist, beträgt 2.28 %.

Schritt 1: Parameter vorbereiten.	σ = 10 cm μ = 1.80 m = 180 cm X1 = 193 cm, X2 = 200 cm Gesucht: P(193 < x ≤ 200)
Schritt 2: Werte in einsetzen.
Schritt 3: z-Wert aus Schritt 2 in Tabelle der Standardnormalverteilung ablesen.	Da wir nun zwei Wahrscheinlichkeiten gegeben haben, müssen wir diese anschließend subtrahieren. = 2.00 = 0.9772 = 1.30 = 0.9032 = 0.9772 – 0.9032 = 0.074
Schritt 4: Wahrscheinlichkeit berechnen.	P = 0.074 * 100 = 7.4 %
Schritt 5: Ergebnis formulieren.	Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person größer ist als 1.93 m, aber höchstens 2.00 m groß ist, beträgt 7.4 %.

Tabelle der Standardnormalverteilung richtig lesen

Wenn du deine Daten standardisiert und den z-Wert bestimmt hast, kannst du in der Tabelle die zugehörige Wahrscheinlichkeit ablesen.

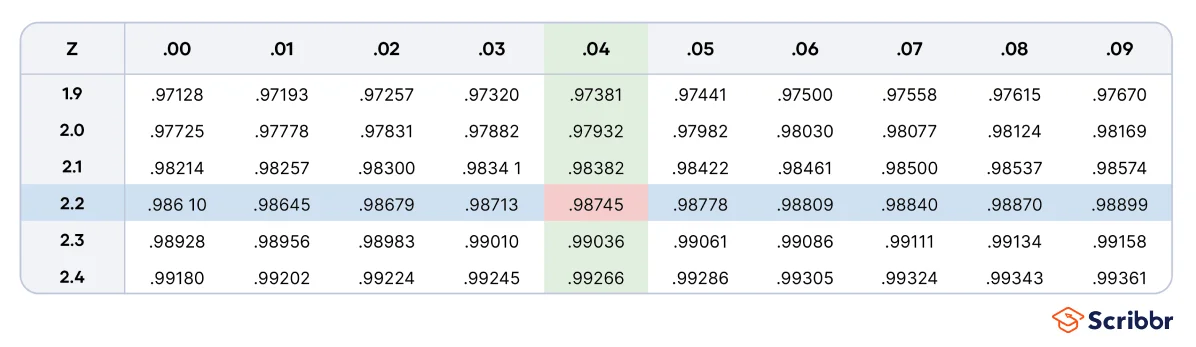
Beim Lesen der Tabelle ist es wichtig zu beachten, dass die ersten zwei Ziffern in der ersten Spalte und die zweite Nachkommastelle in der ersten Zeile dargestellt sind.

Beispiel zur Tabelle der Standardnormalverteilung

Nehmen wir an, wir haben einen z-Wert von 2.24 berechnet. Wir suchen also nach 2.2 in der ersten Spalte an der linken Seite und nach 0.04 in der ersten Zeile und erhalten eine Wahrscheinlichkeit von 0.9874 = 98.74 %. Dieses Beispiel ist in der Tabelle unten rot markiert.

Wichtige z-Werte

Solltest du die Standardnormalverteilung öfter verwenden, merkst du schnell, dass einige z-Werte sehr häufig vorkommen.

So markieren z = 1.96 und z = –1.96 jeweils die 2,5-Prozent-Grenze der Verteilung, das heißt nur 5 % der Daten liegen außerhalb dieses Intervalls.

Folglich können wir also auch sagen, dass 95% aller Werte innerhalb dieses Intervalls liegen.

Außerdem liegen 99% aller z-Werte im Intervall von z = 2.58 und z = –2.58 und 99.9 % aller z-Werte liegen im Intervall von z = 3.29 und z = –3.29.

Diese Werte sind besonders beim Testen von Hypothesen wichtig, da sie häufig als Signifikanzniveau verwendet werden.

Häufig gestellte Fragen

Was ist der Unterschied zwischen Normalverteilung und Standardnormalverteilung?

Die Standardnormalverteilung ist eine besondere Form der Normalverteilung und liegt dann vor, wenn wir eine Normalverteilung mit einem Mittelwert von μ = 0 und einer Standardabweichung von σ = 1 haben.

Was ist die Standardisierung?

Bei der Standardisierung wird eine Normalverteilung in die Standardnormalverteilung umgewandelt. Dabei berechnen wir aus unseren Daten einen z-Wert und können anschließend die Tabelle der Standardnormalverteilung verwenden.

Wie lese ich die Tabelle zur Standardnormalverteilung?

In der Tabelle der Standardnormalverteilung sind die ersten zwei Ziffern des z-Werts in der ersten Spalte und die zweite Nachkommastelle in der ersten Zeile dargestellt.

Hast du zum Beispiel einen Wert von z = 1.26, dann suche zunächst nach 1.2 in der ersten Spalte an der linken Seite und nach 0.06 in der ersten Zeile.

Du erhältst eine Wahrscheinlichkeit von 0.8962 (= 89.62 %).