Die Varianz verstehen und berechnen + Varianz Rechner
Die Varianz gibt an, wie sich deine Beobachtungswerte um den Mittelwert aller Beobachtungen verteilen.
Da sie die Streuung der Werte um den Mittelwert beschreibt, gehört die Varianz zu den Streuungsmaßen. Für das Interpretieren statistischer Ergebnisse in deiner Bachelorarbeit oder deiner Masterarbeit solltest du auch Lageparameter verwenden.
| Person | 1 | 2 | 3 | 4 | 5 |
| Stunden Sport/Woche | 2 | 3 | 7 | 5 | 3 |
Mittelwert:
Varianz:
Varianz Rechner
Du kannst die Varianz von Hand oder mithilfe unseres Varianz Rechners berechnen.
Die Varianz berechnen
| Formel zur Stichprobenvarianz | |
|---|---|
| Varianz | |
| Gesamtzahl der Beobachtungen | |
| Beobachtungswert | |
| arithmetisches Mittel (Mittelwert) der Stichprobe | |
In unseren Beispielen bestimmen wir die Varianz einer Stichprobe, also eines Teils, den wir aus einer Grundgesamtheit entnehmen. Um die Varianz für die Grundgesamtheit zu bestimmen, wird eine leicht andere Formel verwendet.
Für die Berechnung ist es vor allem wichtig, zu beachten, dass wir bei der Varianz für die Grundgesamtheit durch die Gesamtanzahl N und bei der Stichprobenvarianz durch Gesamtanzahl an Beobachtungen minus 1 (n – 1) teilen.
| Formel zur Varianz der Grundgesamtheit | |
|---|---|
| Varianz | |
| Gesamtzahl | |
| Beobachtungswert | |
| arithmetisches Mittel (Mittelwert) der Grundgesamtheit | |
Die Varianz einer Stichprobe in fünf Schritten bestimmen
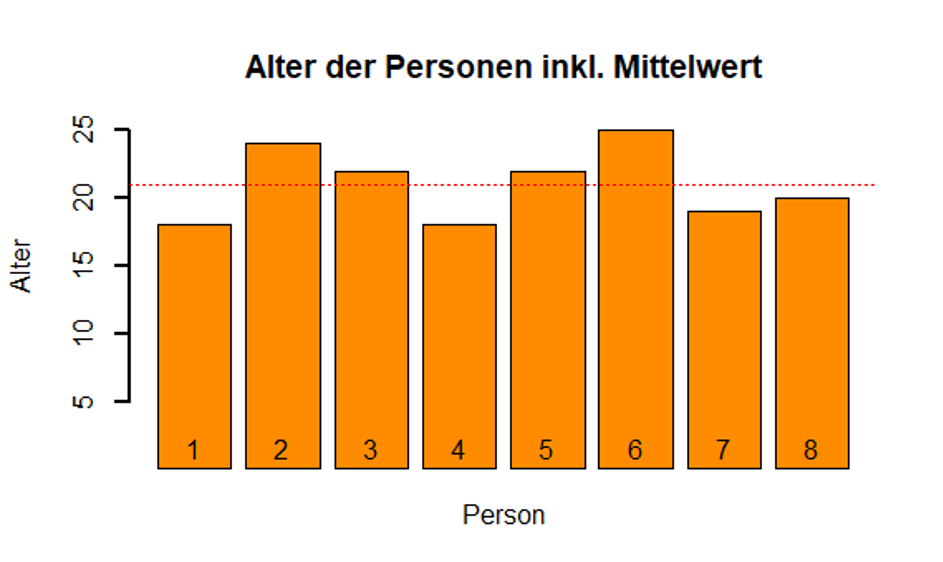
Nehmen wir an, wir haben acht Personen nach ihrem Alter gefragt und folgende Antworten erhalten:
| Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Alter | 18 | 24 | 22 | 18 | 22 | 25 | 19 | 20 |
In der Abbildung sehen wir die Verteilung der verschiedenen Altersangaben der Personen. Die rote Linie zeigt das arithmetische Mittel des Alters in der Gruppe.
| Allgemein | Beispiel | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Bestimme zunächst den Mittelwert x̄ deiner Beobachtungswerte. | Wir berechnen den Mittelwert (x̄), indem wir alle Altersangaben addieren und dann die Summe durch die Gesamtanzahl der Personen teilen.
|
||||||||
| 2 | Berechne nun die Abweichungen der Beobachtungswerte vom Mittelwert.
Subtrahiere dazu den Mittelwert von den einzelnen Beobachtungswerten. |
Nun bestimmen wir die Abweichungen der einzelnen Altersangaben vom Mittelwert x̄ = 21. Dazu ziehen wir den Mittelwert von jeder Altersangabe ab.
|
||||||||
| 3 | Da die Varianz nicht negativ sein kann, quadrieren wir das Ergebnis. | Wir quadrieren die Abweichungen, d. h. wir rechnen (Wert aus Schritt 2)2.
|
||||||||
| 4 | Bilde nun die Summe aus den quadrierten Abweichungen. | Wir addieren alle Ergebnisse aus Schritt 3.
9 + 9 + 1 + 9 + 1 + 16 + 4 + 1 = 50 |
||||||||
| 5 | Nimm die Gesamtanzahl der Beobachtungen minus 1 und teile die Summe aus Schritt 4 durch diese Zahl. | Wir teilen die Summe aus Schritt 4 durch 7, da wir insgesamt acht Personen nach dem Alter gefragt haben.
8 – 1 = 7 |
Von der Varianz zur Standardabweichung
In dem Beispiel sehen wir, dass die Varianz aufgrund der Einheit (z.B. Jahre2) nicht sehr aussagekräftig ist.
Um eine Aussage über die Streuung machen zu können, müssen wir daher zunächst die Standardabweichung aus der Varianz berechnen.
Für unser Beispiel bedeutet dies:
| Varianz | |
|---|---|
| Standardabweichung |
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Die Varianz in Excel berechnen
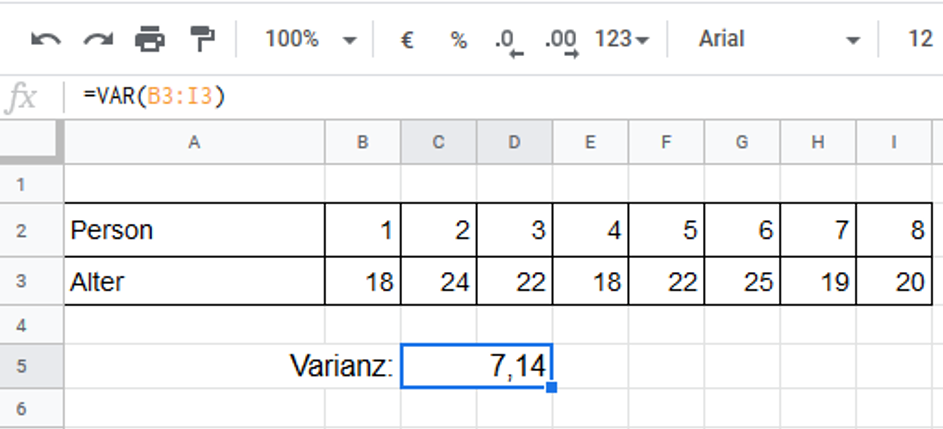
In Excel können wir die Varianz unseres Datensatzes mithilfe der Funktion VARIANZ bestimmen.
Schreibe dazu =VARIANZ oder =VAR und gib in den Klammern die Zellen mit den Werten an, für die du die Varianz bestimmen willst.
Da wir in unserem Beispiel die Varianz aller Altersangaben bestimmen wollen, fügen wir B3:I3 in den Klammern ein und erhalten eine Varianz von 7.14.
Häufig gestellte Fragen
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2023, 02. Mai). Die Varianz verstehen und berechnen + Varianz Rechner. Scribbr. Abgerufen am 9. Juli 2025, von https://www.scribbr.de/statistik/varianz/