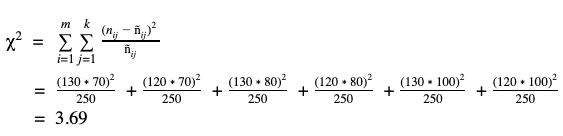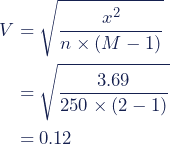Cramers V verstehen, berechnen und interpretieren
Cramers V gibt Auskunft über den statistischen Zusammenhang zwischen zwei oder mehreren nominalskalierten Variablen.
- Der Wert 0 bedeutet, dass es keinen statistischen Zusammenhang gibt.
- Der Wert 1 bedeutet, dass es einen perfekten statistischen Zusammenhang gibt.
In der Praxis liegt Cramers V normalerweise zwischen 0 und 1.
Bei der Bestimmung von Cramers V wird der Chi-Quadrat-Wert (X2) standardisiert. Dadurch kannst du Zusammenhänge zwischen Variablen anhand von Cramers V vergleichen.
Cramers V am Beispiel erklärt
Beispielfrage: Gibt es einen Zusammenhang zwischen Extrovertiertheit und Musikgeschmack?
Im Beispiel wurden 250 Personen befragt, die entweder Rock, Pop oder Klassik als ihr Lieblingsgenre angeben konnten. Die Personen wurden entweder als extrovertiert oder introvertiert klassifiziert.
| Pop | Rock | Klassik | Summe (Zeile) | |
|---|---|---|---|---|
| Extrovertiert | 38 | 35 | 57 | 130 |
| Introvertiert | 32 | 45 | 43 | 120 |
| Summe (Spalte) | 70 | 80 | 100 | 250 |
Für die Berechnung von Cramers V wird der Chi-Quadrat-Wert benötigt. Daher wird dieser zuerst bestimmt. Anschließend kann der Chi-Quadrat-Wert in einen Wert für Cramers V umgewandelt werden.
Im Beispiel is Chi-Quadrat X2 = 3.69.
Genauere Erklärungen zu den einzelnen Berechnungsschritten findest du auch in unserem Artikel zum Chi-Quadrat.
Vom Chi-Quadrat zu Cramers V
Da der Chi-Quadrat-Wert nicht standardisiert und daher nur begrenzt vergleichbar ist, wandelst du ihn in Cramers V um. Anhand dieses Wertes kannst du dann konkrete Schlüsse und Vergleiche ziehen.
 |
|
 |
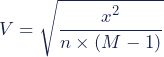Cramers V |
 |
Chi-Quadrat |
 |
Gesamtanzahl (der Stichprobe) |
 |
die kleinere der beiden Zahlen für die Zeilenanzahl ( |
) und die Spaltenanzahl (
), in der KreuztabelleIm Beispiel gibt es zwei Zeilen (Persönlichkeit: extrovertiert/introvertiert) und drei Spalten (Musikgeschmack: Pop/Rock/Klassik). Für M in der Formel zu Cramers V wird wir die kleinere der beiden Anzahlen eingesetzt, im Beispiel also 2.
Für das Beispiel ergibt sich daher Folgendes:
Cramers V richtig interpretieren
Cramers V liegt immer zwischen 0 und 1.
Dabei bedeutet 0, dass es keinen Zusammenhang zwischen den beiden Variablen gibt, und 1, dass es einen perfekten Zusammenhang gibt.
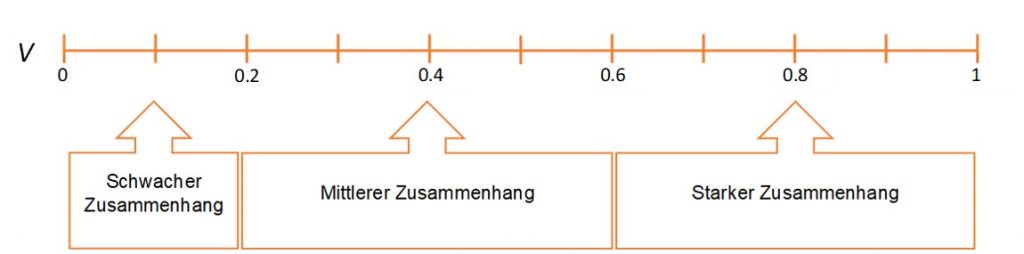
Deinen Wert für Cramers V kannst du anhand dieser Übersicht interpretieren:
| Cramers V | Interpretation |
|---|---|
| V = 0 | kein Zusammenhang |
| V = 0.1 | schwacher Zusammenhang |
| V = 0.3 | moderater Zusammenhang |
| V = 0.5 | starker Zusammenhang |
| V = 1 | perfekter Zusammenhang |
Im Beispiel ist V = 0.12. Es liegt also ein schwacher statistischer Zusammenhang zwischen den Merkmalen Extrovertiertheit und präferierten Musikrichtung vor.
Häufig gestellte Fragen
- Was sagt Cramers V aus?
-
Cramers V gibt uns Auskunft über den statistischen Zusammenhang zwischen zwei oder mehreren nominalskalierten Variablen.
- Was ist der Unterschied zwischen Cramers V und Chi-Quadrat?
-
Cramers V ist ein standardisiertes Zusammenhangsmaß und lässt daher Vergleiche mehrerer Koeffizienten zu. Chi-Quadrat ist nicht standardisiert und hat daher eine geringere Aussagekraft.
- Wie interpretiere ich Cramers V richtig?
-
Der Wert für Cramers V liegt zwischen 0 und 1. Dabei bedeutet 0, dass es überhaupt keinen Zusammenhang gibt, und 1, dass es einen vollständigen Zusammenhang gibt. Dabei gilt es zu beachten, dass wir anhand von Cramers V zwar Aussagen über die Stärke, nicht aber über die Richtung des Zusammenhangs treffen können.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2022, 21. November). Cramers V verstehen, berechnen und interpretieren. Scribbr. Abgerufen am 22. September 2023, von https://www.scribbr.de/statistik/cramers-v/
