Grundgesamtheit in der Statistik + Beispiele
Die Grundgesamtheit (auch Population) ist die gesamte Anzahl an Objekten, über die du Schlüsse ziehen möchtest.
In den Sozialwissenschaften werden meistens Personen untersucht. Die Grundgesamtheit gibt es aber auch in anderen Disziplinen und sie kann sich aus nichtmenschlichen Objekten zusammensetzen.
Eine Grundgesamtheit besteht beispielsweise aus:
- Personen
- Tieren
- Pflanzen
- Firmen
- Ländern
- Organisationen
Die einzelnen Objekte, die Teil der Grundgesamtheit sind, werden statistische Einheiten oder Merkmalsträger genannt.
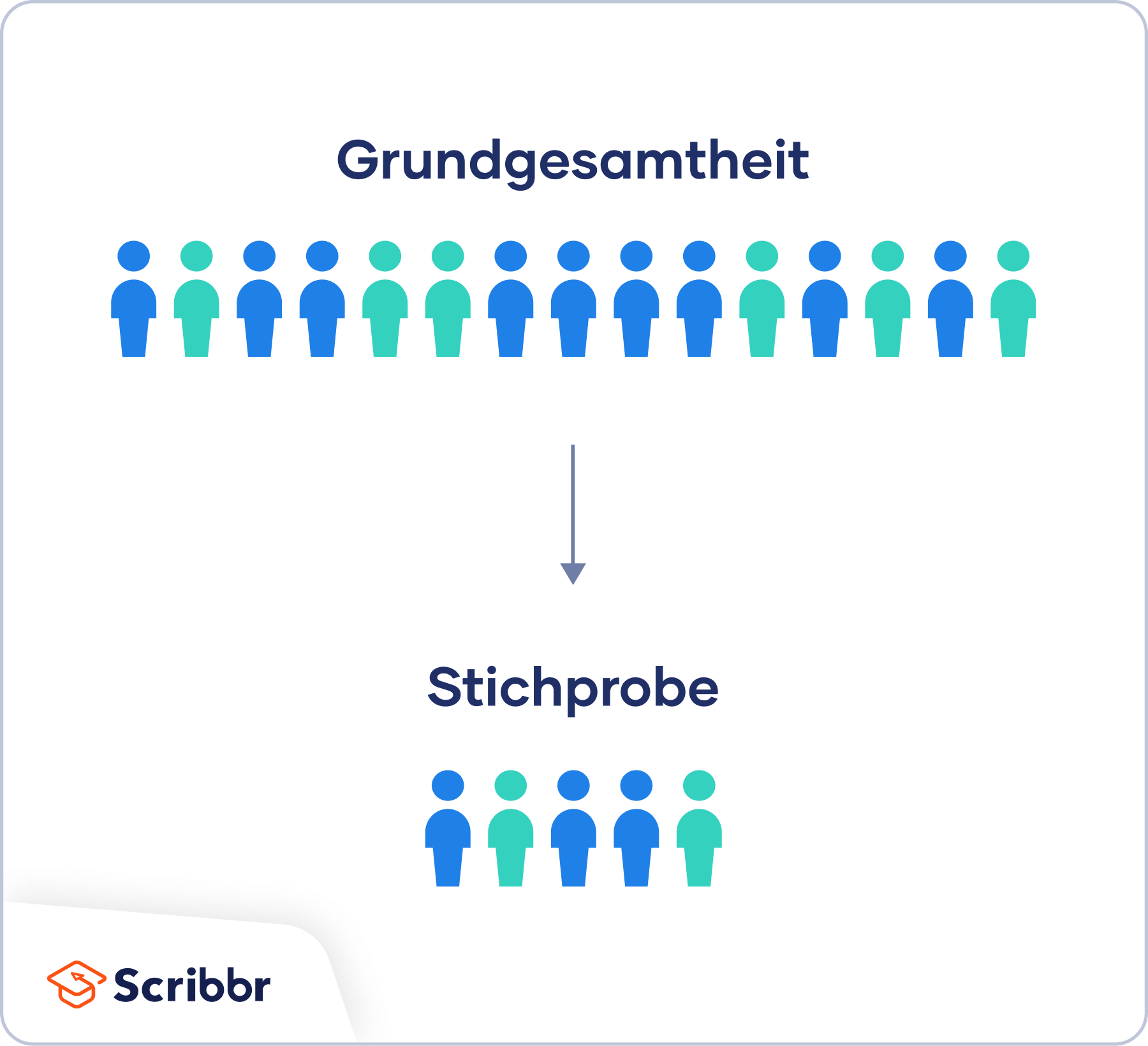
Meist ist es nicht möglich, die vollständige Grundgesamtheit in die Datenerhebung einzubeziehen. Deshalb wird repräsentativ eine Stichprobe aus der Grundgesamtheit untersucht.
Grundgesamtheit: Alle Studierenden, die ihren Master in Deutschland begonnen haben.
Stichprobe: 500 Studierende, die du in deiner Studie befragst.
Grundgesamtheit definieren
Zunächst wird festgelegt, wer tatsächlich zur Grundgesamtheit gehört, über die eine Aussage getroffen werden soll. Die Grundgesamtheit wird dafür anhand von Kriterien definiert. So wird bestimmt, was von der Grundgesamtheit umfasst wird und was nicht.
Die Grundgesamtheit sollte an folgenden Aspekten fixiert werden:
- Räumlich
- Zeitlich
- Sachlich
Fixierung
Räumlich: Eine bestimmte Uni X in Deutschland.
Zeitlich: Alle Studierenden der letzten fünf Jahre.
Sachlich: Ein bestimmter Masterstudiengang.
→ Grundgesamtheit: Alle Studierenden, die in den letzten fünf Jahren ihr Masterstudium an Uni X im Studiengang Y begonnen haben.
So fokussierst du dich auf eine bestimmte Gruppe und kannst valide Schlüsse über diese ziehen. Dies bedeutet jedoch, dass du deine Schlüsse nicht einfach für alle Studierenden generalisieren kannst.
Drei Arten von Grundgesamtheiten
Es gibt drei verschiedene Arten von Grundgesamtheiten:
- Endliche Grundgesamtheiten
- Unendliche Grundgesamtheiten
- Hypothetische Grundgesamtheiten
Endliche Grundgesamtheiten sind zählbar oder berechenbar.
Unendliche Grundgesamtheiten können nicht gezählt oder berechnet werden.
Hypothetische Grundgesamtheiten sind simuliert oder geschätzt.
Unendliche Grundgesamtheit: Alle Fische im Meer. Alle Sterne im Himmel.
Hypothetische Grundgesamtheit: Geschätzte Weltbevölkerung im Jahr 2050.
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Grundgesamtheit untersuchen
Die Grundgesamtheit kann auf zwei Wegen untersucht werden:
Teilerhebungen sind häufig, da es oft nicht möglich ist, die gesamte Grundgesamtheit bei der Datenerhebung zu erfassen. Deshalb werden einige statistische Einheiten aus der Grundgesamtheit ausgewählt: eine Stichprobe.
Anhand dieser Stichprobe werden Schlussfolgerungen über die Grundgesamtheit gezogen. So untersuchst du deine ursprüngliche Annahme über die Grundgesamtheit.
Da die Stichprobe jedoch nicht die ganze Grundgesamtheit umfasst, sind die tatsächlichen Werte und Eigenschaften der Grundgesamtheit nicht bekannt. Deshalb muss herausgefunden werden, ob die Daten der Stichprobe auf die gesamte Grundgesamtheit übertragbar sind.
Dazu wird in der quantitativen Forschung meist per Hypothesentest berechnet, wie wahrscheinlich es ist, dass die Ergebnisse aus der Stichprobe von den wahren Werten der Grundgesamtheit, also deren Eigenschaften, abweichen.
Grundgesamtheit mit Vollerhebung untersuchen
Die Vollerhebung der Grundgesamtheit (auch Totalerhebung) wird durchgeführt, wenn es möglich ist, alle statistischen Einheiten der Grundgesamtheit zu erforschen. Es liegen also entweder Informationen zu allen Datenträgern vor, oder sie können alle untersucht werden.
Grundgesamtheit: Alle Studierenden, die dieses Jahr ihren Master an Uni X begonnen haben.
Vollerhebung: Da im Register der Universität Daten zu allen Studierenden vorliegen, kannst du diese Daten sammeln und eine Vollerhebung der Grundgesamtheit durchführen.
In den meisten Fällen ist es zu aufwendig oder kostspielig, die gesamte Grundgesamtheit zu untersuchen. Denn die Grundgesamtheit ist oft so groß, dass man nicht alle statistischen Einheiten befragen, Daten über sie sammeln oder sie überhaupt erfassen kann.
Je spezifischer die Grundgesamtheit jedoch definiert ist, desto realistischer ist es, eine Vollerhebung durchzuführen. Meist ist dies der Fall, da die Gruppe dann kleiner wird oder einfacher zu untersuchen ist, weil sie greifbarer ist.
Grundgesamtheit mit Teilerhebung untersuchen
Die Teilerhebung wird dann durchgeführt, wenn eine Vollerhebung ausgeschlossen ist. Dabei werden einige statistische Einheiten aus der Grundgesamtheit ausgewählt. Diese sollen repräsentativ für die Grundgesamtheit stehen.
Diese Auswahl nennt sich Stichprobe.
Bei der Teilerhebung ist es wichtig, dass die Stichprobe tatsächlich repräsentativ für die Grundgesamtheit ist. Meist wird dies erfüllt, indem per Zufallsprinzip Objekte aus der Grundgesamtheit für die Stichprobe ausgewählt werden.
Du möchtest anhand der Stichprobe valide Schlüsse über die Grundgesamtheit ziehen. Um das tun zu können, sollten Objekte mit unterschiedlichen Merkmalen innerhalb der Grundgesamtheit gleichermaßen vertreten sein.
Grundgesamtheit: Die Grundgesamtheit sind all diejenigen, die einen Masterstudiengang in Deutschland beginnen.
Teilerhebung: Da es dir nicht möglich ist, alle Studierenden in Deutschland zu befragen, wählst du zufällig 500 Studierende für die Teilnahme an deiner Studie aus.
Damit deine Stichprobe repräsentativ für die Grundgesamtheit ist, achtest du darauf, dass Studierende aus unterschiedlichen Universitäten in ganz Deutschland teilnehmen und aus unterschiedlichen Fakultäten kommen. Innerhalb dieser Kriterien werden die Teilnehmenden zufällig ausgewählt.
Versuche also, alle möglichen unterschiedlichen Untergruppen der Grundgesamtheit gleichmäßig einzubeziehen. Ist dies nicht der Fall, ist die Stichprobe nicht repräsentativ.
Grundgesamtheit: Die Grundgesamtheit sind all diejenigen, die einen Masterstudiengang in Deutschland beginnen.
Teilerhebung: Da du selbst studierst, fragst du einfach die Studierenden, die dir in der Bibliothek deiner Fakultät über den Weg laufen, nach ihrem Alter.
Diese Stichprobe ist nicht repräsentativ für die Grundgesamtheit: Du wählst nur Studierende aus einer bestimmten Fakultät aus. Zudem erhältst du nur das Alter derjenigen, die in die Bibliothek gehen.
→ Möglicherweise weicht das Alter von Studierenden an anderen Fakultäten und denjenigen, die nicht in der Bibliothek lernen, von dem Alter der Studierenden in deiner Stichprobe ab.
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Unterschiede zwischen Grundgesamtheit und Stichprobe
Es ist nicht immer einfach, die Grundgesamtheit und die Stichprobe voneinander zu unterscheiden. Deshalb sind hier noch einmal ein paar Beispiele genannt und die Schreibweise statistischer Symbole aufgelistet, die die Unterscheidung einfacher machen.
Statistische Werte haben unterschiedliche Schreibweisen, wenn es um die Grundgesamtheit oder die Stichprobe geht. Die Grundgesamtheit wird meist mit griechischen Buchstaben notiert, während für die Stichprobe lateinische Buchstaben genutzt werden.
| Grundgesamtheit | Stichprobe | |
|---|---|---|
| Beispiele | ||
| Alle Studierenden im Bachelorstudium in Deutschland | Die 200 Studierenden, die an deiner Studie teilnehmen | |
| Die Wahlberechtigten einer Wahl | Diejenigen, die bei einer Wahlumfrage befragt werden, um eine Prognose zu erstellen | |
| Alle Bücher in einer Bibliothek | Die Bücher, die du aus dem Regal nimmst | |
| Schreibweise | ||
| Generell | Griechische Buchstaben | Lateinische Buchstaben |
| Umfang | N (Gesamtanzahl der statistischen Einheiten in der Grundgesamtheit) | n (Größe der Stichprobe) |
| Durchschnitt (auch: Mittelwert oder arithmetisches Mittel) | μ | x̄ oder M |
| Standardabweichung | σ | s oder SD |
Häufig gestellte Fragen
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Hasselbusch, L. (2023, 15. Februar). Grundgesamtheit in der Statistik + Beispiele. Scribbr. Abgerufen am 14. Juli 2025, von https://www.scribbr.de/statistik/grundgesamtheit/